A constant horizontal force F is applied on the top of a solid sphere and a hallow sphere of same mass and radiuis both kept on a sufficiently rough surface. Let aS and aH be their linear acceleration respectively, then

aS=aH
aS>aH
aS<aH
data sufficient
The correct Answer is:B
Taking torque about contact point. F(2r)=(ICM+mr2)α and ACM=rα.
F(2r)rICM+mr2=ACM As ICM↑,ACM↓aSOLID>aHOLLOW
Similar Questions
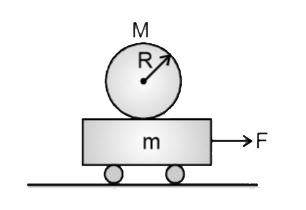
Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μsandμk respectively.
 View Solution
View SolutionA tangential force 'F' is applied at the topmost point of a spherical shell of mass 'm' kept on a rough horizontal surface. If it rolls without slipping, it's acceleration is 6Fxm then 'x'
View Solution
Knowledge Check
- Question 1 - Select One
Torque of equal magnitude is applied to a solid cylinder and a solid sphere, both having the same mass and radius. Both of them are free to rotate about their axis of symmetry. If α1 and α2 are the angular accelerations of the cylinder and the sphere respectively, then the ratio α1α2 will be
A52B54C45D25 - Question 2 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Acceleration of the plank isA3F16mB11F8mC9F4mDZero - Question 3 - Select One
Torques of equal magnitude are applied to a thin hollow cylinder and a solid sphere, both having the same mass and radius. Both of them are free to rotate about their axis of symmetry. If αcandαs are the angular accelerations of the cylinder and the sphere respectively, then the ratio αcαs will be
A52B25C43D34
A solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.
 View Solution
View SolutionP is a solid sphere and Q is a hollow sphere both having the same mass and radius .If they roll down from the top of an inclined plane , on reaching the bottom .
View SolutionConsider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank isView SolutionA solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.
 View Solution
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 View Solution
View Solution

