A solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

F2
3F+29Mgsinθ57
3F+2Mgsinθ19
Coefficient of friction value is not given and hence Cannot be found
The correct Answer is:C
The free body diagram of the plank and the cylinder is as shown in the figure.
For plank, F−f1=2Mgsinθ=2Ma1
For cylinder, f1−f2=Mgsinθ=Ma2
(f1+f2)R=MR22α

For no slipping between plank and cylinder, a2=Rα=a1
For no slipping between cylinder and incline, a2=Rα
After, solving the above equation, f1=3F+2Mgsinθ19
Similar Questions
A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View SolutionA boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
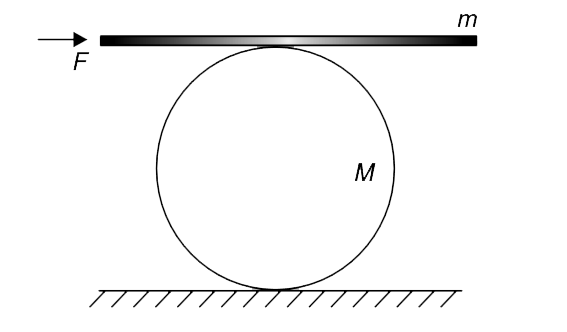 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Consider a cylinder of mass M=1kg and radius R=1mlying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.
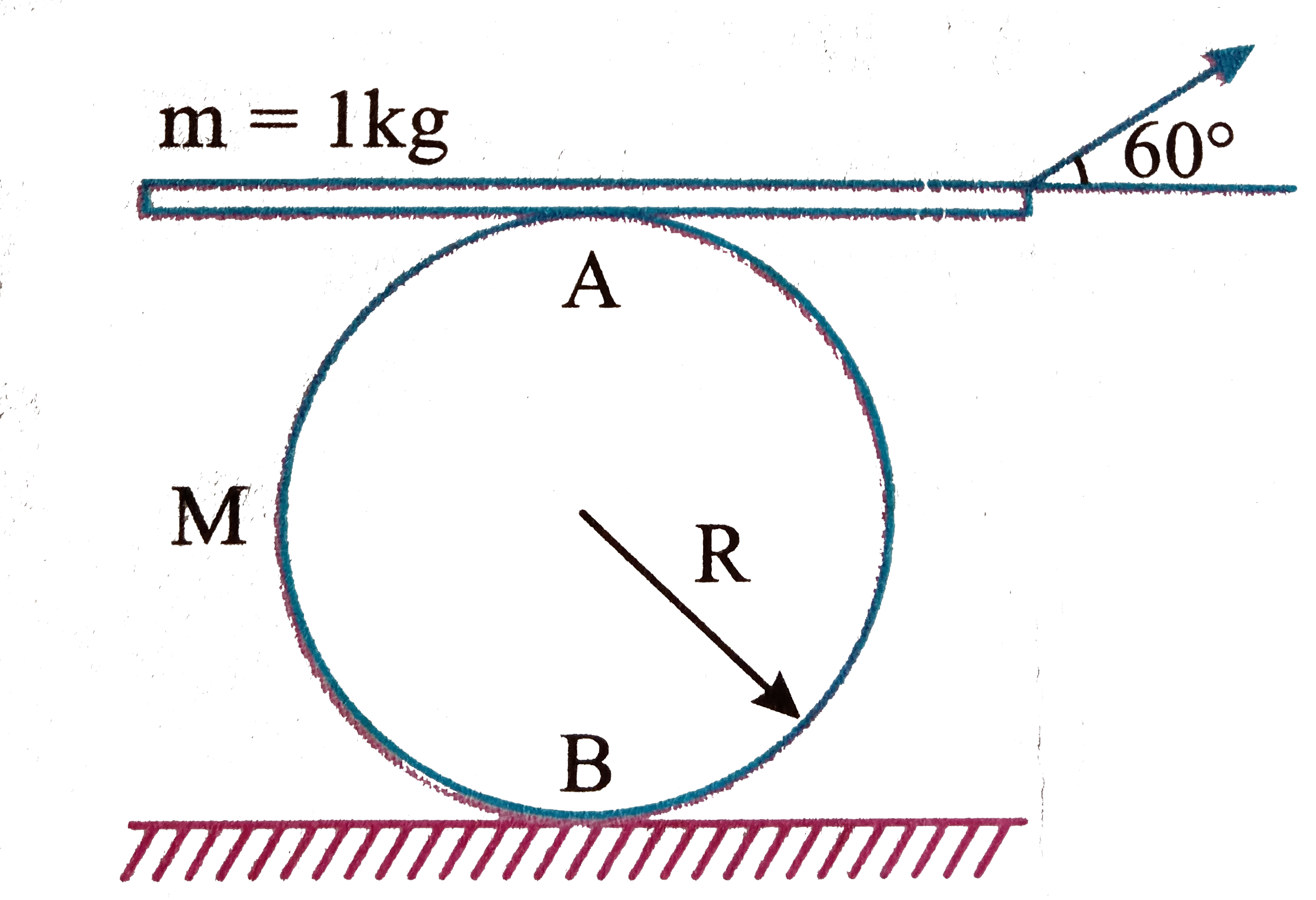
A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The acceleration of cylinder isA20m/s2B10m/s2C5m/s2D12m/s2 - Question 2 - Select One

A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. ThenAangular velocity of the cylinder is vR counter clockwiseBangular velocity of the cylinder is 2vR clockwiseCvelocity of centre of mass of the cylinder is v towards leftDvelocity of centre of mass of the cylinder is 2v towards right. - Question 3 - Select One
Consider a cylinder of mass M=1kg and radius R=1mlying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at A isA7.5NB5.0NC2.5ND1.5N
A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
 View Solution
View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionConsider a cylinder of mass M=1kg and radius R=1mlying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at B isView SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution

