A force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
F(ˆi+ˆj)
−F(ˆi−ˆj)
F(−ˆi−ˆj)
−F(ˆi+ˆj)
The correct Answer is:A
To find the torque of the force ^F acting at the origin O about the point (1,−1), we can follow these steps:
Step 1: Identify the Force and its Position
The force is given as ^F=F^k, which means it acts in the positive z-direction. The point about which we need to calculate the torque is P(1,−1).
Step 2: Determine the Position Vector
The position vector →r from the point P(1,−1) to the origin O(0,0) can be calculated as:
→r=→rfinal−→rinitial=(0,0)−(1,−1)=(−1,1)
Thus, →r=−^i+^j.
Step 3: Write the Force Vector
The force vector is:
→F=F^k
Step 4: Calculate the Torque
The torque →τ is given by the cross product of the position vector →r and the force vector →F:
→τ=→r×→F
Substituting the vectors:
→τ=(−^i+^j)×(F^k)
Step 5: Use the Determinant to Compute the Cross Product
We can use the determinant method to compute the cross product:
→τ=∣∣
∣
∣∣^i^j^k−11000F∣∣
∣
∣∣
Step 6: Calculate the Determinant
Calculating the determinant:
→τ=^i∣∣∣100F∣∣∣−^j∣∣∣−100F∣∣∣+^k∣∣∣−1100∣∣∣
Calculating each of these determinants:
- For ^i: 1⋅F−0⋅0=F
- For ^j: −1⋅F−0⋅0=−F
- For ^k: −1⋅0−1⋅0=0
Thus, we have:
→τ=F^i+F^j+0^k=F^i+F^j
Final Result
The torque about the point (1,−1) is:
→τ=F(^i+^j) Newton meter
The force is given as ^F=F^k, which means it acts in the positive z-direction. The point about which we need to calculate the torque is P(1,−1).
The position vector →r from the point P(1,−1) to the origin O(0,0) can be calculated as:
→r=→rfinal−→rinitial=(0,0)−(1,−1)=(−1,1)
Thus, →r=−^i+^j.
The force vector is:
→F=F^k
The torque →τ is given by the cross product of the position vector →r and the force vector →F:
→τ=→r×→F
→τ=(−^i+^j)×(F^k)
We can use the determinant method to compute the cross product:
→τ=∣∣
∣
∣∣^i^j^k−11000F∣∣
∣
∣∣
Calculating the determinant:
→τ=^i∣∣∣100F∣∣∣−^j∣∣∣−100F∣∣∣+^k∣∣∣−1100∣∣∣
Calculating each of these determinants:
- For ^i: 1⋅F−0⋅0=F
- For ^j: −1⋅F−0⋅0=−F
- For ^k: −1⋅0−1⋅0=0
→τ=F^i+F^j+0^k=F^i+F^j
The torque about the point (1,−1) is:
→τ=F(^i+^j) Newton meter
Similar Questions
Find the torque of forces about O
(a)
(b)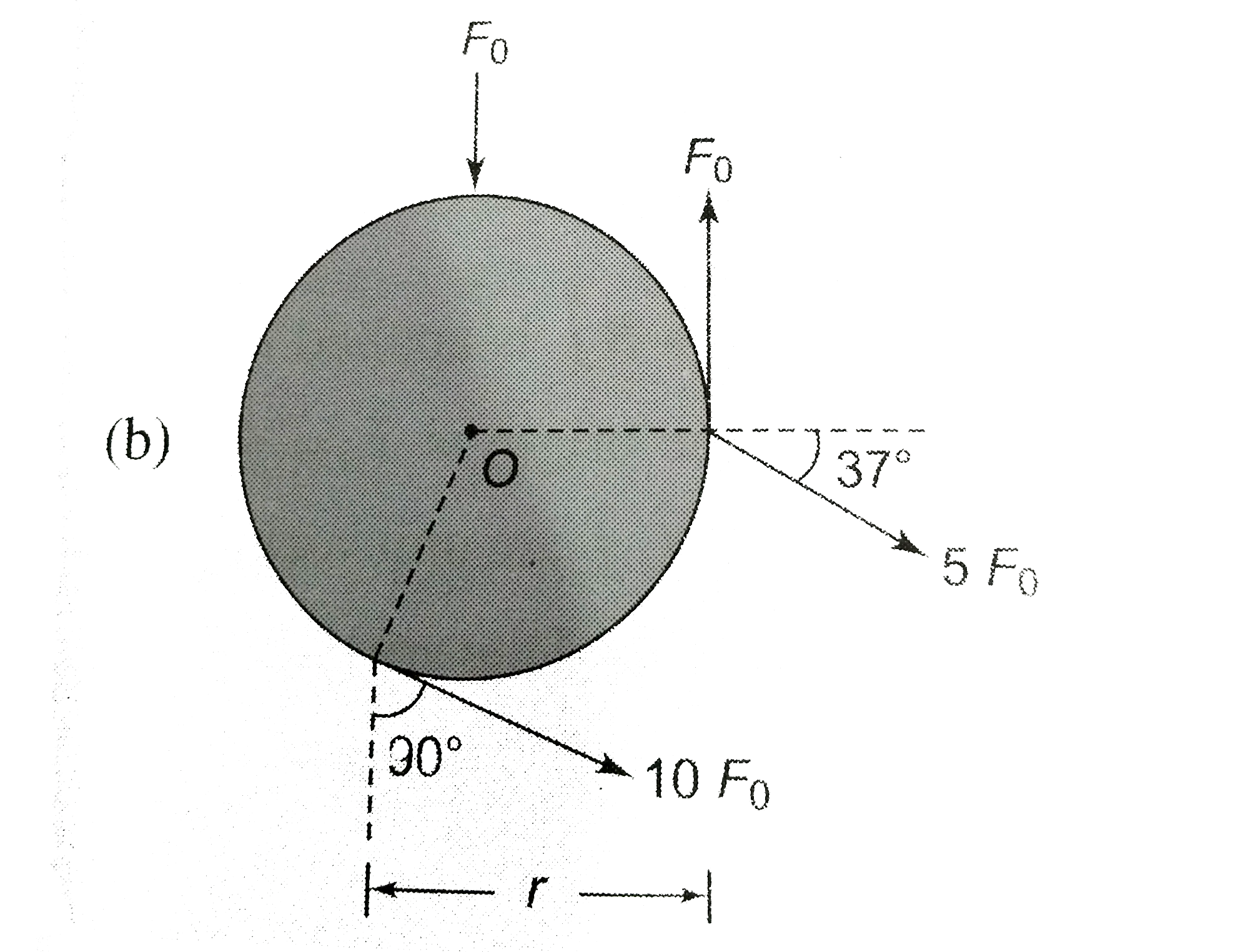
View SolutionLet a force F be acting on a body free to rotate about a point O and let r be the position vector of any point P on the line of action of the force. Then torque (τ) of this force about point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m. Find the torque of this force.
View Solution
Knowledge Check
A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −Fˆk actgs on O, the origin of the coodinate system. The torque about the point (1,-1) is
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
A force of −4FˆK acts O, the origin of the coordinate system. The torque about the point (1,−1) is
View SolutionA force of −Fˆk on O, the origin of the coordinate system. The torque about the point (1,−1) is.
.
View SolutionIf is the force acting on a particle having position vector and be the torque of this force about the origin, then-
View SolutionStatement-I : Magnitude of torque of a force about a given point does not depend upon the location of the origin of the co-ordinate system.
Statement II: Moment of couple is different for different points in its plane
View SolutionForce ˆi+2ˆj−3ˆk,2ˆi+3ˆj+4ˆk and −ˆi−ˆj+ˆk are acting at the point P(0,1,2) . The moment of these forces about the point A(1,-2,0) is
View Solution