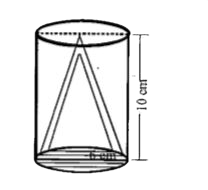
From a right circular cylinder with height $10 c m$ and radius of base $6 c m$ , a right circular cone of the same height and base is removed. Find the volume of the remaining solid.

Video Solution

Text Solution

Verified by Experts

Given, Height of cylinder $h = 10 c m$ .
Radius of the base $r = 6 c m$
Required volume $=$ Volume of cylinder $-$ Volume of cone
$\Rightarrow π r^{2} h - (\frac{1}{3}) π r^{2} h$
$\Rightarrow (\frac{22}{7}) \times {(6)}^{2} \times 10 - (\frac{1}{3}) \times (\frac{22}{7}) \times {(6)}^{2} \times 10$
$\Rightarrow (\frac{22}{7}) \times [360 - 120]$
$\Rightarrow (\frac{22}{7}) \times [240]$
$\Rightarrow 754.28 c m^{3}$

|

Updated on:21/07/2023

Class 9 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A $240 π$ cu. cm
B5280 cu. cm
C $620 π$ cu. cm
D $360 π$ cu. cm
Question 2 - Select One
From a right circular cylinder of radius 10 cm and height 21 cm, a right circular cone of same base radius is removed. If the volume of the remaining portion is $4400 c m^{3}$ , then the height of the removed cone (taking $π = \frac{22}{7}$ ) is :
A15 cm
B18 cm
C21 cm
D24 cm
Question 3 - Select One
Volume of a right circular cylinder of height 21 cm and base radius 5 cm is :
A $1255 c m^{3}$
B $1050 c m^{3}$
C $1175 c m^{3}$
D $1650 c m^{3}$

RD SHARMA-SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER-All Questions

Home
Ask Doubt
Profile