Let f(x)=|||x|−1|−1|andg(x)−(maxf(t):x≤t≤x+1,x∈R} The graph of g(x) is symmetrical about
Step by step video & image solution for Let f(x)=|||x|-1|-1| and g(x)-(max f(t): x leq t leq x+1, x in R} The graph of g (x) is symmetrical about by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let f(x)={1−|x|,|x|≤10,|x|>1andg(x)=f(x−1)for allx∈R The graph for g(x) is given by
A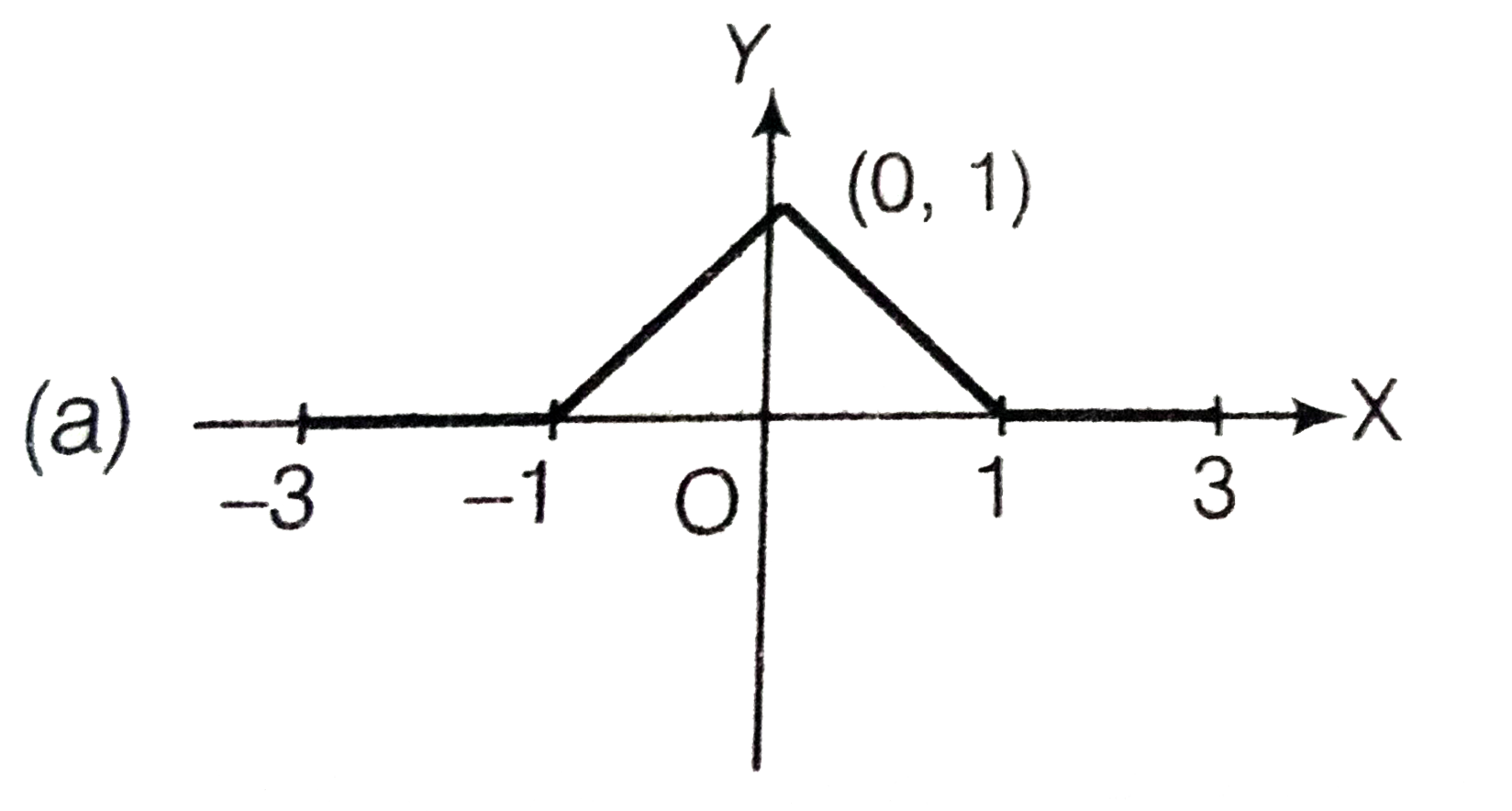 B
B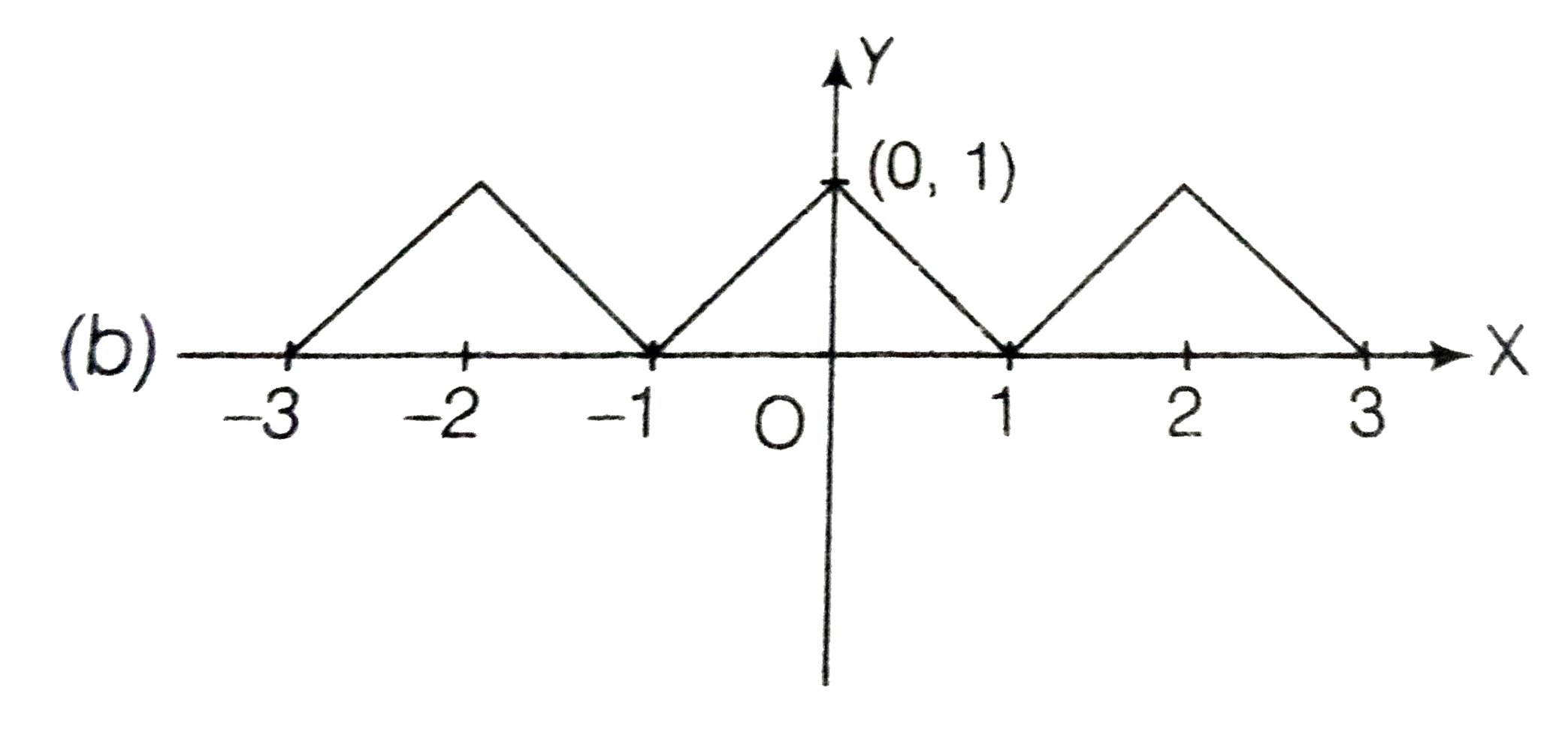 C
C D
D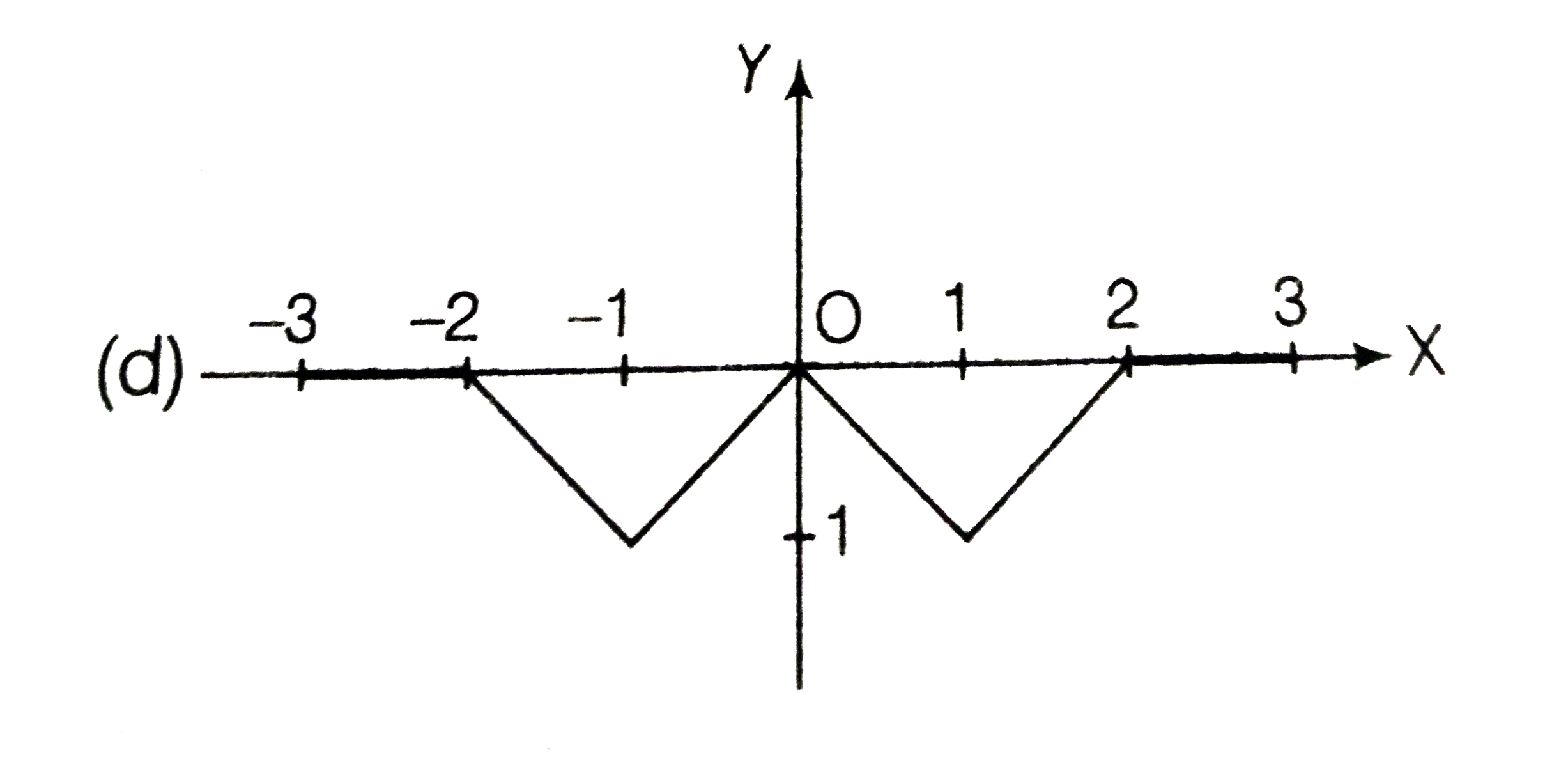
Let f(x)=x3−x2+x+1 and g(x)={max f(t)0≤t≤x0≤x≤13−x1<x≤2 then
Ag(x) is discontinuous at x=1Bg(x) is continuous at x=1Cg(x) is differentiable at x=1Dg(x) is non differentiable at x=1Suppose f and g are differentiabel functions such that xg(f(x))f'(g(x))g'(x)=(g(x))g'(f(x))f'(x)∀x∈Randf is positive ∀n∈R. Also ∫x0f(g(t))dt=12(1−e−2x)∀x∈R,g(f(0))=1andh(x)=g(f(x))f(g(x))∀x∈R.
The graph of y=h(x) is symmetric with respect to line:Ax=−1Bx=0Cx=1Dx=2
If f(x)+f(1−x)=2 and g(x)=f(x)−1∀x∈R, then g(x) is symmetric about
View SolutionSuppose f and g are differentiabel functions such that xg(f(x))f'(g(x))g'(x)=f(g(x))g'(f(x))f'(x)∀x∈Randf is positive ∀n∈R. Also ∫x0f(g(t))dt=12(1−e−2x)∀x∈R,g(f(0))=1andh(x)=g(f(x))f(g(x))∀x∈R.
The graph of y=h(x) is symmetric with respect to line:
View Solutionlet (f(x)=1−|x|,|x|≤1,0,|x|>1) g(x)=f(x+1)+f(x−1)
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View Solution
