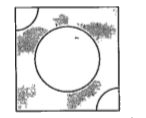
From each of the two opposite corners of a square of side 8cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of diameter 4.2cm is also cut from the centre as shown in figure. Find the area of the remaining (shaded) portion of the square.
Side of square = 8 cm
Area of square=(side)2=82=64cm2
Quadrant circle of radius r=1.4 cm
Area of quadrant circle =(14)(π×r2)=(14)×(227)×(1.4)2=1.54cm2
Diameter of bigger circle= 4.2 cm
∴ Radius of bigger circle R= 2.1 cm
Area of bigger circle=(π×R2)=(227)×(2.1)2=55.44cm2
area of the remaining portion of the square= Area of square - 2(Area of quadrant circle) - Area of bigger circle
area of the remaining portion of the square= 64−(2×1.54)−55.44
area of the remaining portion of the square=5.48cm2
Topper's Solved these Questions
Similar Questions
From a square of side 8 cm, two quadrants of a circle of radii 1.4 cm are cut from two corners. Another circle of radius 4.2 cm is also cut from the centre as shown in the figure. Find the area of the remaining (shaded) portion of the square. [Take π=227]
 View Solution
View SolutionFrom a square of side 8 cm, two quadrants of a circle of radii 1.4 cm are cut from two corners . Another circle of radius 4.2 cm is also cut from the centre as shown in the figure . Find the area of the remaining (shaded) portion of the square . [Takeπ=227]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the area of shaded portion if each side of the square is 14 cm.
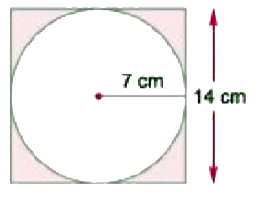 A50 sq cmB45 sq cmC62 sq cmD42 sq cm
A50 sq cmB45 sq cmC62 sq cmD42 sq cm - Question 2 - Select One
Find the area of a square inscribed in a circle of radius 4 cm.
A32 sq cmB18 sq cmC64 sq cmD25 sq cm
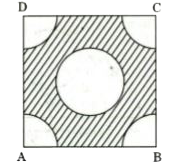
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionIn the given figure ABCD is a square of side 4cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region.
[Use π=3.14]
 View Solution
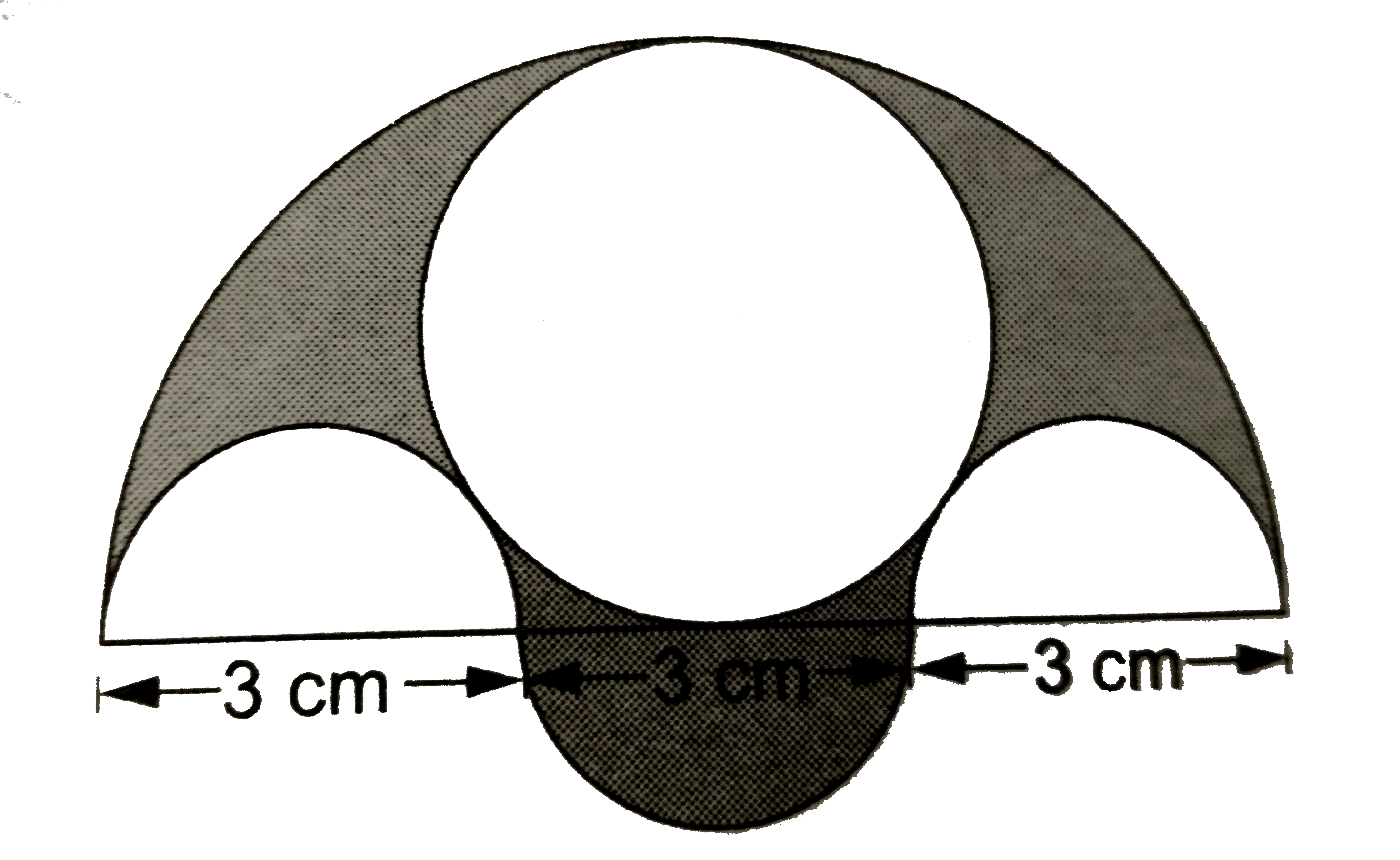
View SolutionThree semicirles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region.
 View Solution
View SolutionIn the figure given below, ABCD is a square of side 4 cm. Quadrants of a circle of diameter 2 cm are removed from the four corners and a circle of diameter 2 cm is also removed. What is the area of the shaded region ?
 View Solution
View SolutionFour equal circles are described about the four corners of square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
 View Solution
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.
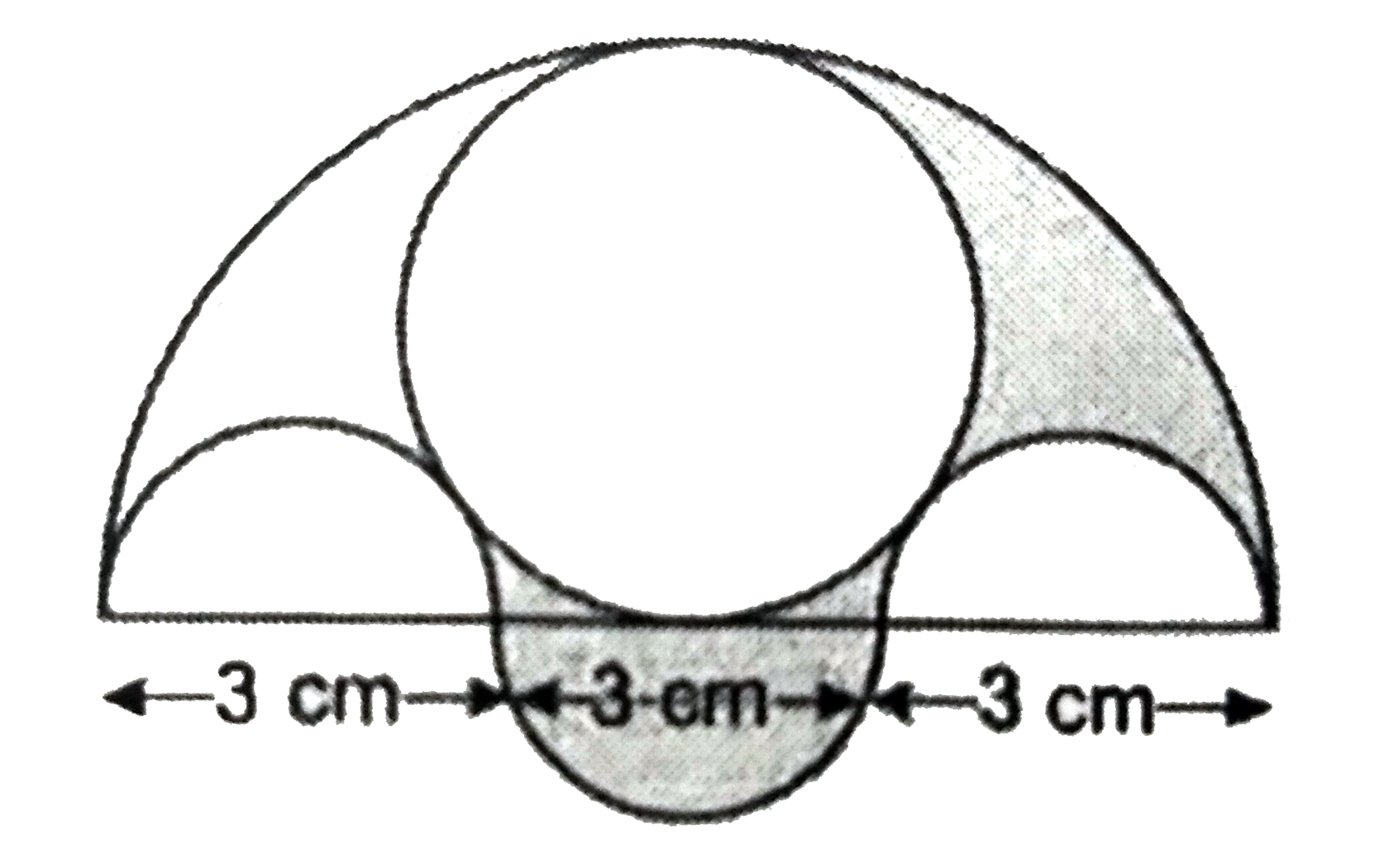 View Solution
View Solution

