Find the potential at the centre of a square of side √2 m . Which carries at its four corners charges q1=3×10−6C,q2=−3×10−6C,q3=−4×106C,q4=7×10−6C.
2.7×104V
1.5×103V
3×102V
5×103V
The correct Answer is:A
To find the electric potential at the center of a square with charges placed at its corners, we follow these steps:
Step 1: Identify the configuration
We have a square of side length √2 m with the following charges at the corners:
- q1=3×10−6C
- q2=−3×10−6C
- q3=−4×10−6C
- q4=7×10−6C
Step 2: Calculate the distance from the center to a corner
The distance r from the center of the square to any corner can be calculated using the Pythagorean theorem. Since the side of the square is √2, each half of the side (from the center to a corner) is:
r=√22√2=1m
Step 3: Use the formula for electric potential
The electric potential V at a point due to a point charge is given by:
V=kqr
where k is Coulomb's constant (k≈8.99×109N m2/C2), q is the charge, and r is the distance from the charge to the point of interest.
Step 4: Calculate the total potential at the center
Since the potential is a scalar quantity, we can sum the potentials due to each charge:
Vtotal=V1+V2+V3+V4=k(q1r+q2r+q3r+q4r)
Substituting r=1m:
Vtotal=k(q1+q2+q3+q4)
Step 5: Substitute the values of the charges
Now substituting the values of the charges:
Vtotal=k(3×10−6−3×10−6−4×10−6+7×10−6)
Calculating the sum:
Vtotal=k(3−3−4+7)×10−6=k(3×10−6)
Step 6: Calculate the potential
Now substituting k:
Vtotal=8.99×109×3×10−6=26.97×103V=2.697×104V
Final Result
The potential at the center of the square is approximately:
V≈2.7×104V
We have a square of side length √2 m with the following charges at the corners:
- q1=3×10−6C
- q2=−3×10−6C
- q3=−4×10−6C
- q4=7×10−6C
The distance r from the center of the square to any corner can be calculated using the Pythagorean theorem. Since the side of the square is √2, each half of the side (from the center to a corner) is:
r=√22√2=1m
The electric potential V at a point due to a point charge is given by:
V=kqr
where k is Coulomb's constant (k≈8.99×109N m2/C2), q is the charge, and r is the distance from the charge to the point of interest.
Since the potential is a scalar quantity, we can sum the potentials due to each charge:
Vtotal=V1+V2+V3+V4=k(q1r+q2r+q3r+q4r)
Substituting r=1m:
Vtotal=k(q1+q2+q3+q4)
Now substituting the values of the charges:
Vtotal=k(3×10−6−3×10−6−4×10−6+7×10−6)
Calculating the sum:
Vtotal=k(3−3−4+7)×10−6=k(3×10−6)
Now substituting k:
Vtotal=8.99×109×3×10−6=26.97×103V=2.697×104V
The potential at the center of the square is approximately:
V≈2.7×104V
Similar Questions
Three charges q1,q2 and q3 are shown in figure . Determine the net force acting on charge q1 . The charges and separation are given as q1=−1.0×10−6C,q2=+3.0×10−6C, and q3=−2.0×10−6C,r12=15cm,r13=10cm and θ=30∘.

View SolutionFour point charges q1,q2,q3 and q4 are placed at the corners of the squares of side a,as shown in figure.Calculate the potential at the centre of the square.
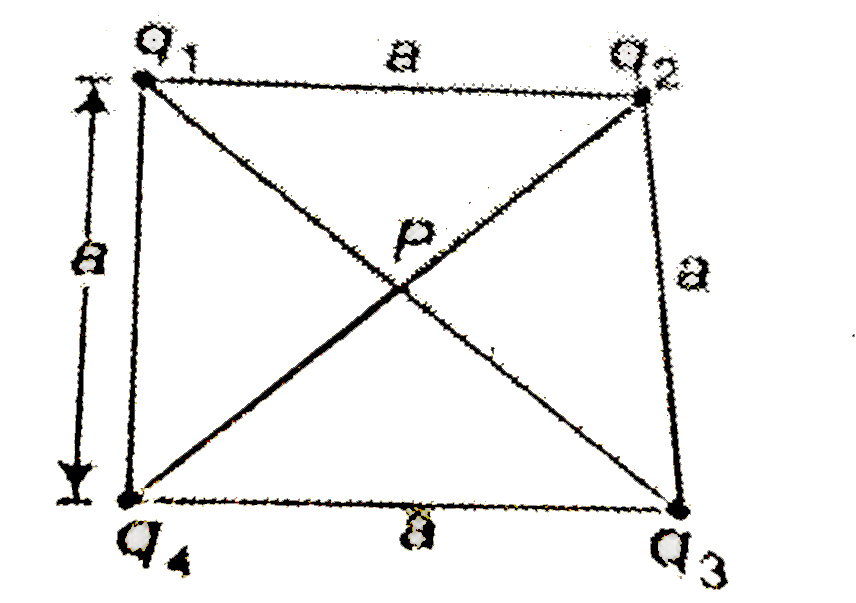
(Given, q1=1×10−8C,q2=−2×10−8C,q3=3×10−8C,q4=2×10−8C and a=1m)
View Solution
Knowledge Check
Light of wavelength 4000Å falls on a photosensitive metal and a negative 2V potential stops the emitted electrons. The work function of the material ( in eV) is approximately (h=6.6×10−34Js,e=1.6×10−19C,c=3×108ms−1)
A1.1B2.0C2.2D3.1Determine the gravitational potential on the surface of earth, given that radius of the earth is 6.4×106m: its mean density is 5.5×103kgm−3,G=6.67×10−11Nm2kg−2.
A−6.297×107Jkg−1B3.11×1011Jkg−1C4×108Jkg−1D−2×109Jkg−1
What is the potential at the centre of a square of each side 1.0 meter, when four charges +1×10−8C,−2×10−8C,+3×10−8Cand+2×10−8C are placed at the four corners of the square.
View SolutionWhat is the electrostatic potential energy of the charge configuration shown in figure. Take q1=+1.0×10−8C,q2=−2.0×10−8C,q3=+3.0×10−8C,q4=+2.0×10−8Canda=1.0metre.
View SolutionCalculate the magnitude and direction of the electric field at a point P which is 30 cm to the right of a point charge Q=−3.0×10−6C
View SolutionThe value of charge on the oil droplets experimentally observed were−1.6×10−19,−2.4×10−19and−4×10−19 C. The value of electronic charge, indicated by these results is
(1) −1.6×10−19
(2) −2.4×10−19
(3) −4×10−19
(4) -0.8×10−19
View SolutionFind the capacitance of a capacitor having a charge of 6×10−7C and energy of 4.5×10−4J
View SolutionFind the potential at centre of square having charges 2×10−9C,+1×10−9C,−2×10−9Cand3×10−9C at the four corners. The side of the square is √2m.
View Solution
