For the second order reaction, concentration (x) of the product at time t starting with initial concentration [A]o is :
kt[Ao]21+kt[Ao]
k[Ao]21+kt
1+kt[Ao]2k+[Ao]2
None of these
The correct Answer is:A
To derive the expression for the concentration (x) of the product at time t for a second-order reaction starting with an initial concentration (A)0, we can follow these steps:
Step 1: Write the rate law for a second-order reaction
For a second-order reaction, the rate of reaction can be expressed as:
Rate=k(A)2
where k is the rate constant and (A) is the concentration of reactant A.
Step 2: Use the integrated rate law for a second-order reaction
The integrated rate law for a second-order reaction is given by:
1(A)−1(A)0=kt
where (A)0 is the initial concentration of A, and (A) is the concentration at time t.
Step 3: Express (A) in terms of x
Let x be the concentration of the product formed at time t. Therefore, the concentration of A at time t can be expressed as:
(A)=(A)0−x
Step 4: Substitute (A) into the integrated rate law
Substituting (A)=(A)0−x into the integrated rate law gives:
1(A)0−x−1(A)0=kt
Step 5: Simplify the equation
Rearranging the equation:
1(A)0−x=kt+1(A)0
Taking the reciprocal of both sides:
(A)0−x=1kt+1(A)0
Step 6: Solve for x
Now, solving for x:
x=(A)0−1kt+1(A)0
To combine the terms, we can rewrite it as:
x=(A)0−(A)0kt(A)0+1
This can be simplified to:
x=(A)0(kt(A)0)kt(A)0+1
Final Expression
Thus, the concentration of the product x at time t for a second-order reaction is:
x=kt(A)201+kt(A)0
For a second-order reaction, the rate of reaction can be expressed as:
Rate=k(A)2
where k is the rate constant and (A) is the concentration of reactant A.
The integrated rate law for a second-order reaction is given by:
1(A)−1(A)0=kt
where (A)0 is the initial concentration of A, and (A) is the concentration at time t.
Let x be the concentration of the product formed at time t. Therefore, the concentration of A at time t can be expressed as:
(A)=(A)0−x
Substituting (A)=(A)0−x into the integrated rate law gives:
1(A)0−x−1(A)0=kt
Rearranging the equation:
1(A)0−x=kt+1(A)0
Taking the reciprocal of both sides:
(A)0−x=1kt+1(A)0
Now, solving for x:
x=(A)0−1kt+1(A)0
To combine the terms, we can rewrite it as:
x=(A)0−(A)0kt(A)0+1
This can be simplified to:
x=(A)0(kt(A)0)kt(A)0+1
Thus, the concentration of the product x at time t for a second-order reaction is:
x=kt(A)201+kt(A)0
Similar Questions
Knowledge Check
- Question 1 - Select One
For a second order reaction, half-life concentration of reactants:
AIndependent of initial concentration of reactantsBDirectly proportional to concentration of reactantsCInversely proportional to concentration of reactantsDInversely proportional to the square of concentration of reactants - Question 2 - Select One
In a first order reaction the concentration of product ’x’ at time 't' is given by the expression (a=initial concentration, k=rate constant, n=order)
Ax=a(1−e−kt)Bx=1a−xCx=12n−1Dx=aa−x - Question 3 - Select One
For an irreversible chemical reaction, the concentration of the products with time
AincreaesBdecreasesCdoes not changeDsome more data required
For a first order reaction :
A→B with initial concentration =aView SolutionIn a 1st order reaction, reactant concentration C varies with times t as:
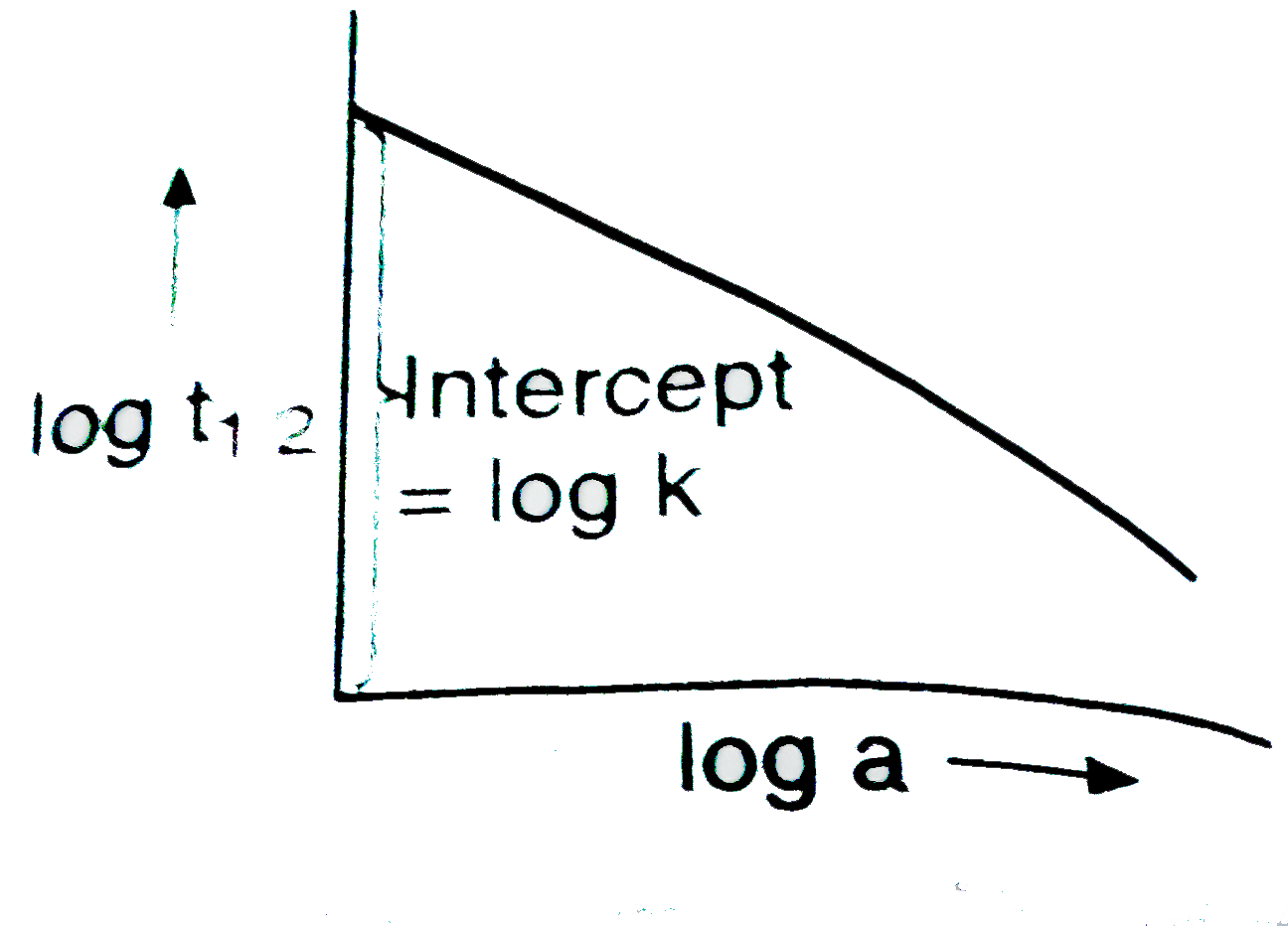
View SolutionFor a second order reaction, 2A→ Products, a plot of log t1/2 vs log a (where a is initial concentration) will give an intercept equal to which one of the following?
 View Solution
View SolutionFor a first order reaction : A→nB (with n-possibly fractional), the concentration of the product varies with time as (A0 is the concentration of A at time t=0).
View SolutionFor a zero order reaction '[R]0 is the initial concentration
View Solution

