2A→B+C
The mechanism of the above reaction given as
2AK1⇐⇒K2X+2B (fast)
X+BK3−−→C (slow)
E1= Activation energy for K1
K2= Activation energy for K2
E3=Activation energy for K3
Calculate Ereaction
(given : E1=10kJ,E3=5kJ,E2=12kJ)
5
6
7
3
The correct Answer is:D
To calculate the activation energy of the overall reaction given the mechanism, we can follow these steps:
Step 1: Identify the Rate-Determining Step
The slow step in the provided mechanism is the rate-determining step (RDS). This means that the rate of the overall reaction is determined by this step. In this case, the slow step is:
X+BK3→C
Step 2: Write the Expression for the Rate
The rate of the reaction can be expressed in terms of the concentration of the reactants involved in the rate-determining step:
Rate=K3(X)(B)
Step 3: Use the Equilibrium Expression
The first step of the mechanism is an equilibrium step:
2AK1⇌K2X+2B
From this equilibrium, we can express the concentration of the intermediate (X):
Keq=(X)(B)2(A)2=K1K2
Thus, rearranging gives:
(X)=K1K2(A)2(B)2
Step 4: Substitute (X) into the Rate Equation
Substituting the expression for (X) into the rate equation gives:
Rate=K3(K1K2(A)2(B)2)(B)
This simplifies to:
Rate=K1K3K2(A)2(B)−1
Step 5: Determine the Effective Rate Constant
From the above expression, we can identify the effective rate constant Keffective:
Keffective=K1K3K2
Step 6: Calculate the Activation Energy of the Overall Reaction
When combining rate constants, the activation energies behave as follows:
- If rate constants are multiplied, their activation energies add.
- If rate constants are divided, the activation energies subtract.
Thus, the activation energy for the overall reaction Ereaction can be calculated as:
Ereaction=E1+E3−E2
Step 7: Substitute the Given Values
Now, substituting the given values:
- E1=10kJ
- E2=12kJ
- E3=5kJ
We get:
Ereaction=10+5−12=3kJ
Final Answer
Thus, the activation energy for the overall reaction is:
3kJ
---
The slow step in the provided mechanism is the rate-determining step (RDS). This means that the rate of the overall reaction is determined by this step. In this case, the slow step is:
X+BK3→C
The rate of the reaction can be expressed in terms of the concentration of the reactants involved in the rate-determining step:
Rate=K3(X)(B)
The first step of the mechanism is an equilibrium step:
2AK1⇌K2X+2B
From this equilibrium, we can express the concentration of the intermediate (X):
Keq=(X)(B)2(A)2=K1K2
Thus, rearranging gives:
(X)=K1K2(A)2(B)2
Substituting the expression for (X) into the rate equation gives:
Rate=K3(K1K2(A)2(B)2)(B)
This simplifies to:
Rate=K1K3K2(A)2(B)−1
From the above expression, we can identify the effective rate constant Keffective:
Keffective=K1K3K2
When combining rate constants, the activation energies behave as follows:
- If rate constants are multiplied, their activation energies add.
- If rate constants are divided, the activation energies subtract.
Ereaction=E1+E3−E2
Now, substituting the given values:
- E1=10kJ
- E2=12kJ
- E3=5kJ
Ereaction=10+5−12=3kJ
Thus, the activation energy for the overall reaction is:
3kJ
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - SOLVED EXAMPLE (SUBJECTIVE)24videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise -1 (Introduction, Rate of reaction, Factor affecting rate of reaction, Effect of concentration on reaction rate)9videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)1videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 420videos
CHEMICAL EQUILIBRIUM
- BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry22videos
CLASSROOM PROBLEMS
Similar Questions
In the sequence of reaction
AK1−−→BK2−−→CKc−−→D,K3>K2>K1 then the rate determining step of the reaction isView SolutionFor the two parallel reactions Ak1−−→BandAk2−−→C, show that the activation energy E' for the disappearance of A is given in terms of activation energies E1andE2 for the two paths by
E'=k1E1+k2K2k1+k2View Solution
Knowledge Check
- Question 1 - Select One
A reactant (A) forms two products AK1−−→B, Activation energy Ea1AK1−−→C , Activation energy Ea2 If Ea1=2Ea2 , then K1 and K2 are related as
AK1=2K2eKa2/RTBK1=K2eKa1/RTCK2=K1eEa2/RTDdCdt=K[A][B]2 - Question 2 - Select One
A reactant (A) forms two products
Ak1−−→B, Activation energy Ea1
Ak2−−→C, Activation energy Ea2
If Ea2=2Ea1 then k1 and k2 are related asAk1=2k2eEa2/RTBk1=k2eEa1/RTCk2=k1eEa2/RTDk1=Ak2eEa1/RT - Question 3 - Select One
Reactant (A) forms two products :
Ak1−−→B Activation energy,Ea1
Ak2−−→C Activation energy,Ea2
If Ea2=2Ea1, then ky and ky are related asAk2=k1eEa1/RTBk2=k1eEa2/RTCk1=Ak2eEa1/RTDk1=2k2eEa2/RT
A reactant (A) forms two products
Ak1−−→B, Activation energy Ea1
Ak2−−→C, Activation energy Ea2
If Ea2=2Ea1 then k1 and k2 are related asView SolutionA reactant (A) forms two products :
Ak1−−→B activation energy Ea1
Ak2−−→C activation energy Ea2
If Ea2=2Ea1, then k1 and k2 will be related asView SolutionReactant (A) forms two products :
Ak1−−→B Activation energy, Ea1
Ak2−−→C Activation energy, Ea2
If Ea2=2Ea2, and k1 and k2 are related asView SolutionA reactant (A) froms two products,
Ak1−−→B, Activation Energy Ea1
Ak2−−→B, Activation Energy Ea2
If Ea1=2Ea2, then k1andk2 are related as:View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
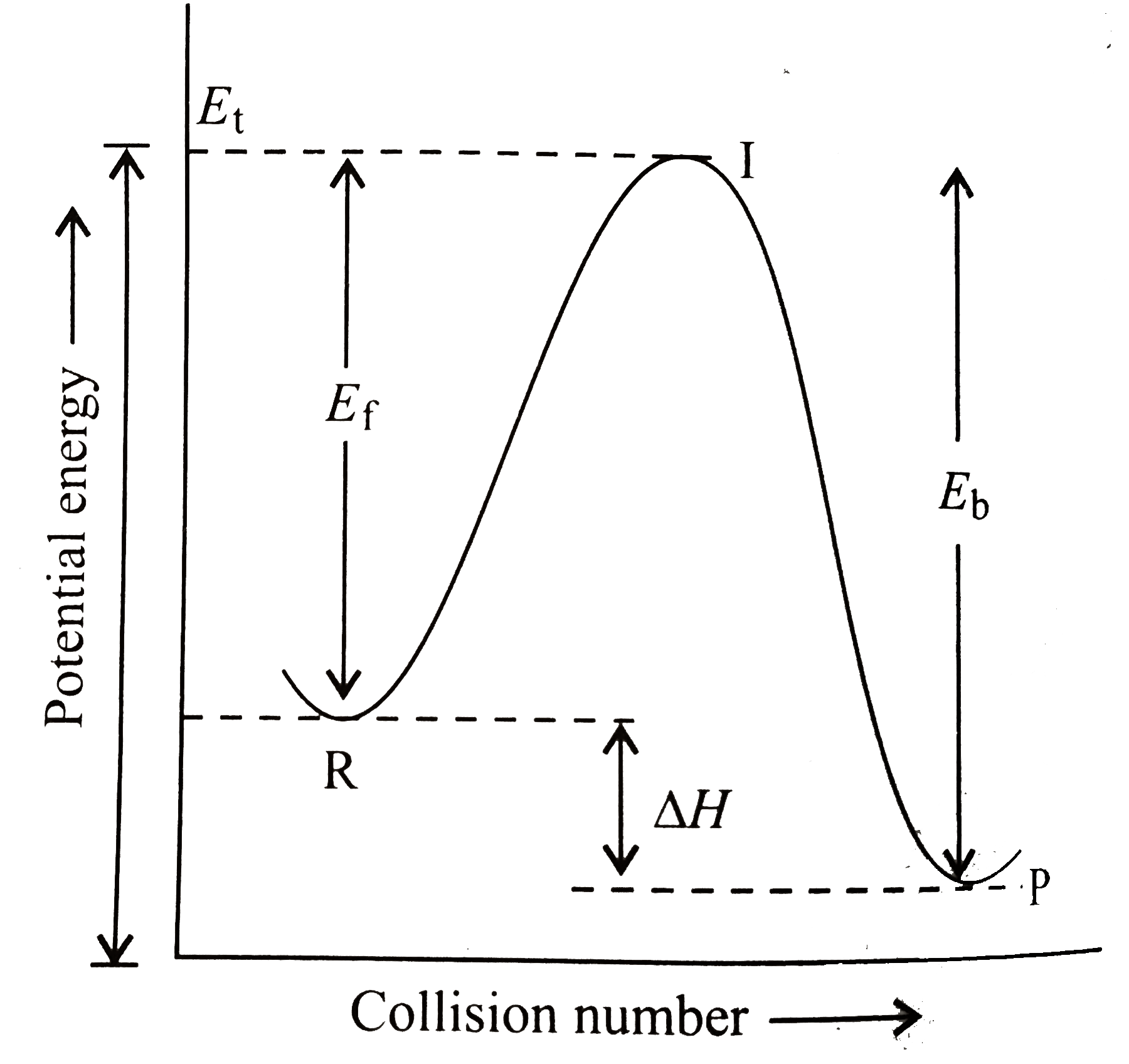
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, thenView Solution

