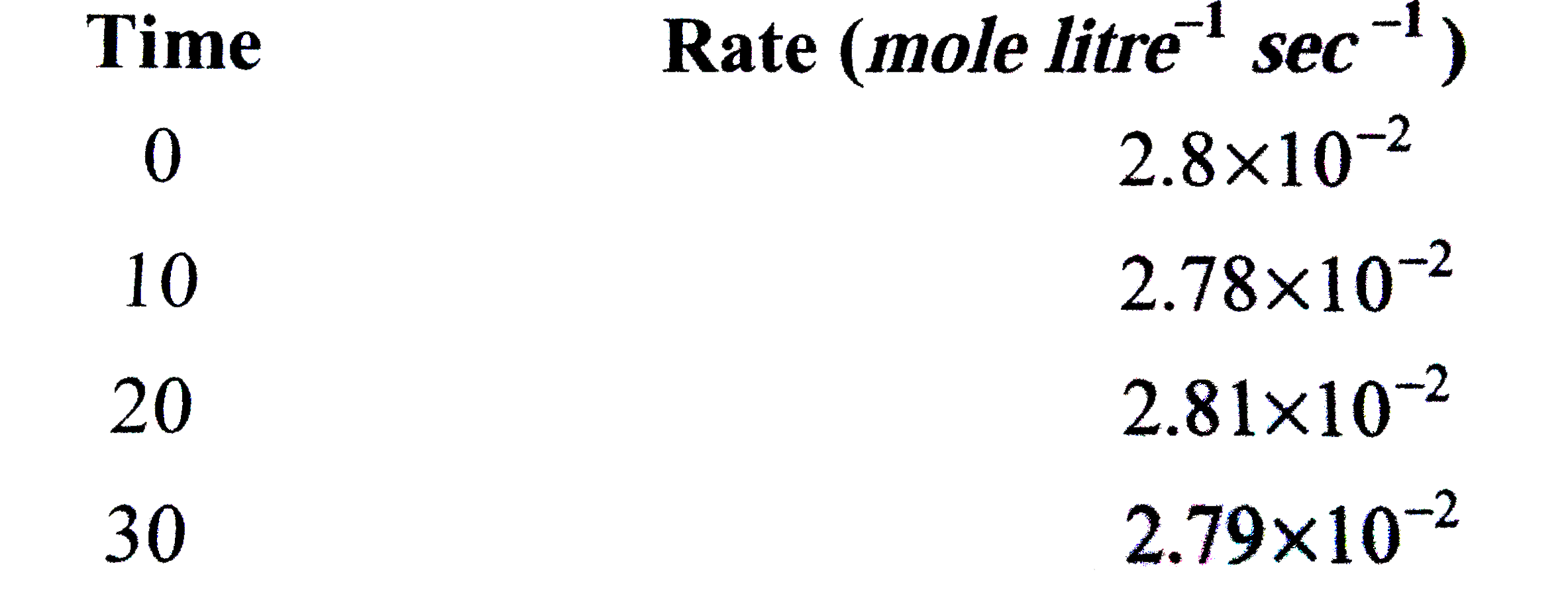For the reaction A→ Product, −d[A]dt=k and at different time interval, [A] values are :

At 20 minute, rate will be :
12 mol /min
10 mol/min
8 mol/min
0.4 mol/min
The correct Answer is:D
Step by step video & image solution for For the reaction A rarr" Product, "-(d[A])/(dt)=k and at different time interval, [A] values are : At 20 minute, rate will be : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise -1 (Methods to monitor the progress of reaction)
4 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise -1 (Arrhenius equation)
6 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise -1 (Zero order reaction, 1st order reaction , 2nd order reaction & nth order reaction)
11 Videos
- CHEMICAL EQUILIBRIUMBOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 4
20 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry
22 Videos
Similar Questions
Knowledge Check
For the reaction A→ Product, −d[A]dt=k and at different time interval, [A] values are :

At 20 minute, rate will be :A12 mol/minB10 mol/minC8 mol/minD0.4 mol/minFor the reaction A→ Product, −d[A]dt=k and at different time interval, [A] values are :

At 20 minute, rate will be :A12 mol/minB10 mol/minC8 mol/minD0.4 mol/minIn the reaction, 3A → 2B rate of reaction, +d[B]dt is equal to
A−13d[A]dtB−23d[A]dtC+2d[A]dtD−32d[A]dt
If for the reaction A→B rate=−d[A]dt=2d[B]dt then, rate law is
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionFor the reaction A+B+C→ products , the term (−d[C]/dt) in rate equation refers to
View SolutionFor a reation: A→ Product,
rate law is −d[A]dt=K[A]0.
The concentration of A left after time t when t=1K is:
View SolutionFor a reaction 2A + B → product, rate law is −d[A]dt=k[A]. At a time when t=1k, concentration of the reactant is " (C0=initial concentration)
View Solution