An optically active compound A upon acid catalysed hydrolysis yield two optically active compound B and C by pseudo first order kinetics. The observed rotation of the mixture after 20 min was 5∘ while after completion of the reaction it was –20∘. If optical rotation per mole of A, B & C are 60∘,40∘&–80∘. Calculate half life of the reaction.
The correct Answer is:20
To solve the problem step by step, we need to analyze the information given and apply the principles of chemical kinetics and optical activity.
Step 1: Understand the Reaction
The reaction involves an optically active compound A undergoing acid-catalyzed hydrolysis to yield two optically active products B and C. The rotation of the mixture changes over time, indicating the progress of the reaction.
Step 2: Gather Given Data
- Observed rotation after 20 minutes: α20=5∘
- Observed rotation after completion of the reaction: α∞=−20∘
- Optical rotation per mole:
- A: αA=60∘
- B: αB=40∘
- C: αC=−80∘
Step 3: Set Up the Equation for Optical Rotation
The observed rotation at any time can be expressed as:
αt=αA⋅(n0−x)+αB⋅nB+αC⋅nC
Where:
- n0 = initial moles of A
- x = moles of A that have reacted
- nB and nC are the moles of B and C formed.
At completion:
α∞=αB⋅nB+αC⋅nC
Step 4: Calculate Moles of B and C
At completion, all of A has reacted:
- If n0 moles of A yield nB moles of B and nC moles of C, we can express:
α∞=nB⋅40+nC⋅(−80)
Since nB+nC=n0, we can express nC in terms of nB:
nC=n0−nB
Substituting this into the equation gives:
−20=nB⋅40+(n0−nB)(−80)
Simplifying this equation will help us find the relationship between nB and n0.
Step 5: Solve for Moles
Rearranging the equation:
−20=40nB−80n0+80nB
−20=120nB−80n0
120nB=80n0−20
nB=80n0−20120=2n0−163
Step 6: Use the Observed Rotation After 20 Minutes
Using the observed rotation after 20 minutes:
5=n0⋅60−x⋅60+nB⋅40+nC⋅(−80)
Substituting nC and nB into this equation will allow us to express x in terms of n0.
Step 7: Calculate the Rate Constant k
Using the pseudo first-order kinetics, we can express the rate constant k using the integrated rate law:
ln(n0n0−x)=kt
Where t=20 minutes. We can find k from the change in optical rotation.
Step 8: Calculate Half-Life
The half-life t1/2 for a first-order reaction is given by:
t1/2=0.693k
Substituting the value of k will give us the half-life of the reaction.
Final Answer
After performing the calculations, we find that the half-life of the reaction is 20 minutes.
---
The reaction involves an optically active compound A undergoing acid-catalyzed hydrolysis to yield two optically active products B and C. The rotation of the mixture changes over time, indicating the progress of the reaction.
- Observed rotation after 20 minutes: α20=5∘
- Observed rotation after completion of the reaction: α∞=−20∘
- Optical rotation per mole:
- A: αA=60∘
- B: αB=40∘
- C: αC=−80∘
The observed rotation at any time can be expressed as:
αt=αA⋅(n0−x)+αB⋅nB+αC⋅nC
Where:
- n0 = initial moles of A
- x = moles of A that have reacted
- nB and nC are the moles of B and C formed.
α∞=αB⋅nB+αC⋅nC
At completion, all of A has reacted:
- If n0 moles of A yield nB moles of B and nC moles of C, we can express:
α∞=nB⋅40+nC⋅(−80)
Since nB+nC=n0, we can express nC in terms of nB:
nC=n0−nB
Substituting this into the equation gives:
−20=nB⋅40+(n0−nB)(−80)
Simplifying this equation will help us find the relationship between nB and n0.
Rearranging the equation:
−20=40nB−80n0+80nB
−20=120nB−80n0
120nB=80n0−20
nB=80n0−20120=2n0−163
Using the observed rotation after 20 minutes:
5=n0⋅60−x⋅60+nB⋅40+nC⋅(−80)
Substituting nC and nB into this equation will allow us to express x in terms of n0.
Using the pseudo first-order kinetics, we can express the rate constant k using the integrated rate law:
ln(n0n0−x)=kt
Where t=20 minutes. We can find k from the change in optical rotation.
The half-life t1/2 for a first-order reaction is given by:
t1/2=0.693k
Substituting the value of k will give us the half-life of the reaction.
After performing the calculations, we find that the half-life of the reaction is 20 minutes.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-II) (COMPREHENSION - 3)4videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-II) (COMPREHENSION - 4)5videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-II) (Zero order reaction, 1st order reaction, 2nd order reaction & nth order reaction)9videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 420videos
CHEMICAL EQUILIBRIUM
- BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry22videos
CLASSROOM PROBLEMS
Similar Questions
An optically active compound A is hydrolysed by dilute acid to give two optically active compounds, B and C according to the following chemical equation, A+H2O→2B+C. The angle of rotation after 40 minutes was observed to be 26∘ and that after completion of reaction was 10∘ at 27∘C. Find the half-time of the reaction assuming it to follow pseudo first order kinetics. The observed rotation per mole of A, B and C are 60∘ , 50∘ and −80∘. A plot of logarithm of rate constant of the above reaction vs T−1 give straight line with intercept equal to 15.046 on log k axis. Calculate at what temperature half-time of the reaction will be 31.1 min.
View SolutionThe first order reaction:
Sucrose → Glucose + Fructose takes place at 308K in 0.5NHCl. At time zero the initial total rotation of the mixture is 32.4∘. After 10min, the total rotation is 28.8∘. If the rotation of sucrose per mole is 85∘, that of glucose is 7.4∘, and of fructose is −86.04∘, calculate the half life of the reaction.View Solution
Knowledge Check
- Question 1 - Select One
A first order reaction is 50% completed in 20 minutes at 27∘C and in 5 min at 47∘C. The energy of activation of the reaction is
A43.85 kJ/molB55.14 kJ/molC11.97 kJ/molD6.65 kJ/mol - Question 2 - Select One
A first order reaction is 50% completed in 20 minutes at 27∘ C and in 5 minutes at 47∘ . The energy of activation of the reaction is :
A43.85 KJ/molB55.14 KJ/molC11.97 KJ/molD6.65 KJ/mol - Question 3 - Select One
Optically active isomer (A) of (C5H9Cl) on treatment with one mole of H2 gives an optically inactive compound (B) compound (A) will be :
A B
B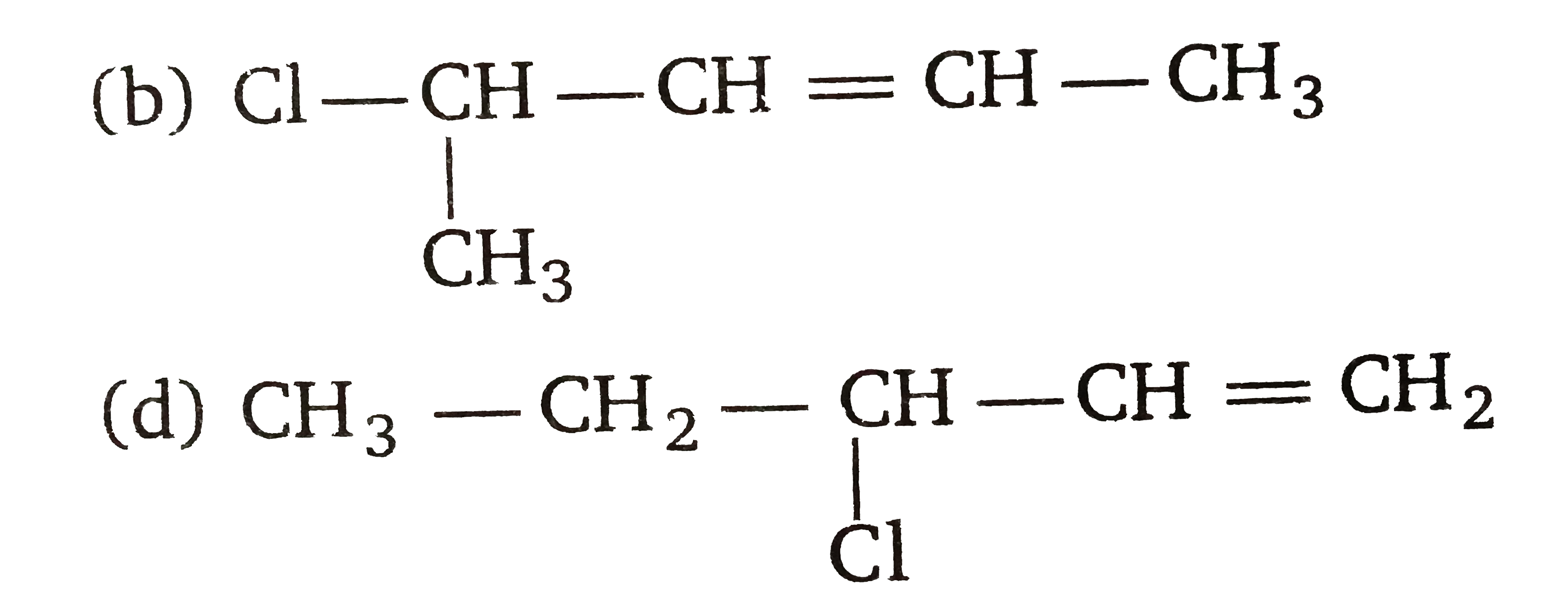 C
C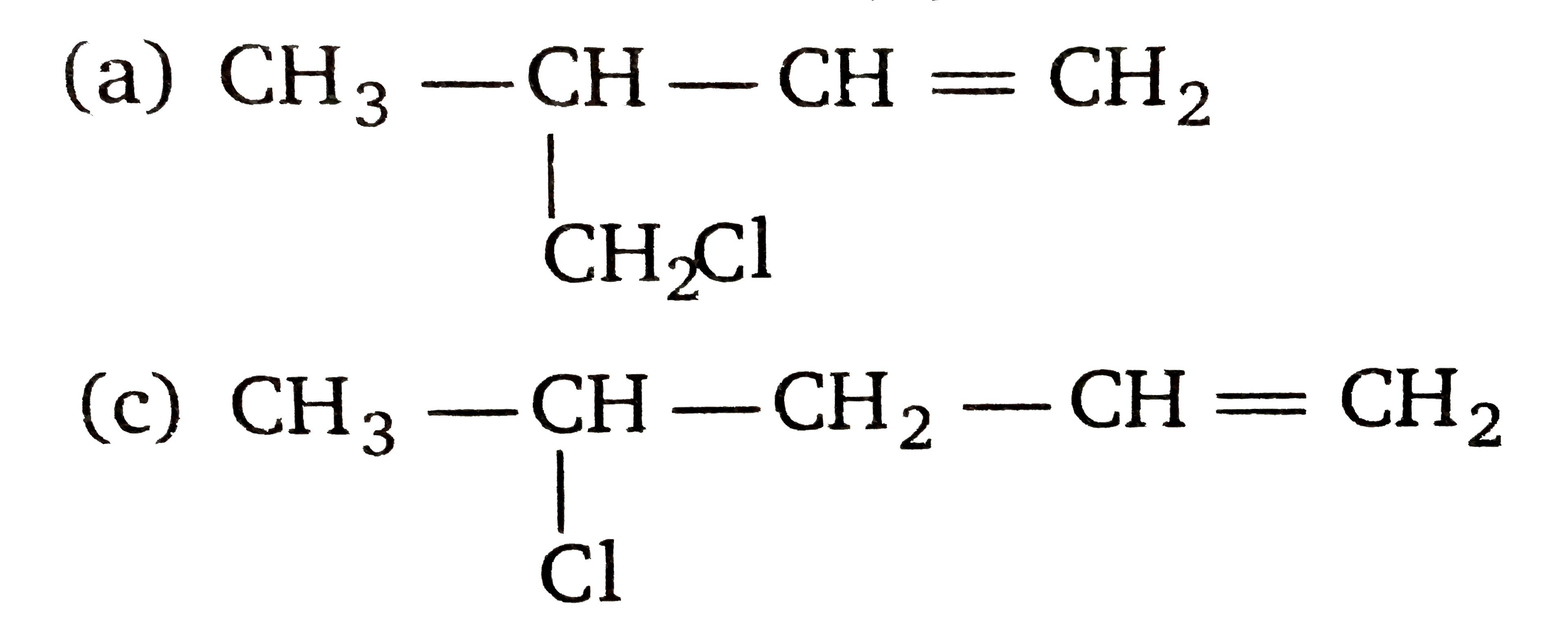 D
D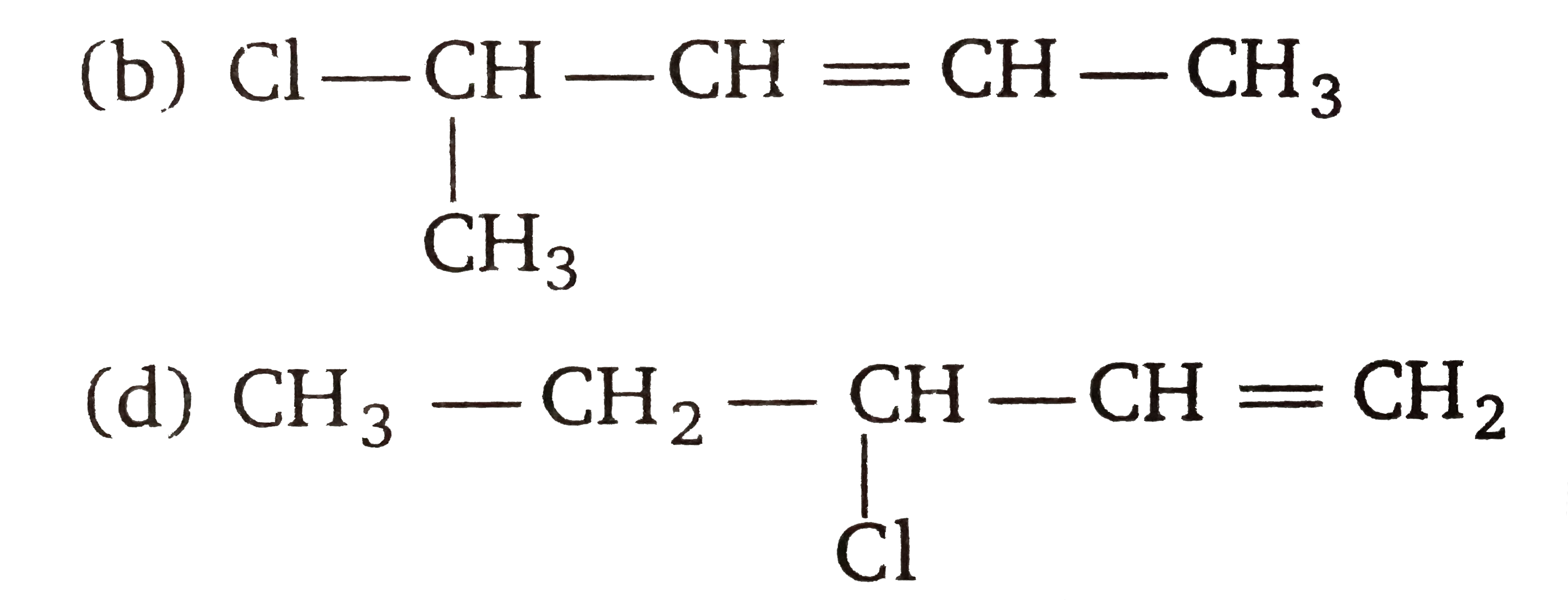
The first order reaction : Sucrose ⇒ Glucose + Fructose take place at 308 K in 0.5N HCl. At time zero the initial total rotation of the mixture is 32.4∘. After 10 minutes the total rotation is 28.8∘. If the rotation of sucrose per mol is 85∘, that of glucose is 74∘ and fructose is −86.04∘. Calculate the half life of the reaction.
View Solution75% of a first order reaction is completed in 30min. Calculate (a) half life, (b) rate constant and (c) time required for 99.9% completion of the reaction
View SolutionAn optically active compound having molecular formula C7H15Br reacts with aqueous KOH to give a racemic mixture of products write the mechanism involved in the reaction.
View SolutionThe first order reaction:
Sucrose → Glucose + Fructose takes place at 308K in 0.5NHCl. At time zero the initial total rotation of the mixture is 32.4∘. After 10min, the total rotation is 28.8∘. If the rotation of sucrose per mole is 85∘, that of glucose is 7.4∘, and of fructose is −86.04∘, calculate the half life of the reaction.View SolutionA first order reaction is 50% completed in 30min at 27∘C and in 10min at 47∘C. Calculate the reaction rate constants at 27∘C and the energy of activation of the reaction in kJmol−1.
View Solution

