In a vertical U-tube containing a luquid, the two arms are maintained at different temperatures, t1 and t2 . The liquid coplumns in the two arms have heights l1 and l2 respectively. The coefficient of volume expansion of the liquid is equal to

The correct Answer is:l1−l2l1(T2−T1)
Step by step video, text & image solution for In a vertical U-tube containing a luquid, the two arms are maintained at different temperatures, t_(1) and t_(2) . The liquid coplumns in the two arms have heights l_(1) and l_(2) respectively. The coefficient of volume expansion of the liquid is equal to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT24videos
HEAT AND THERMAL EXPANSION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO66videos
HEAT TRANSFER
Similar Questions
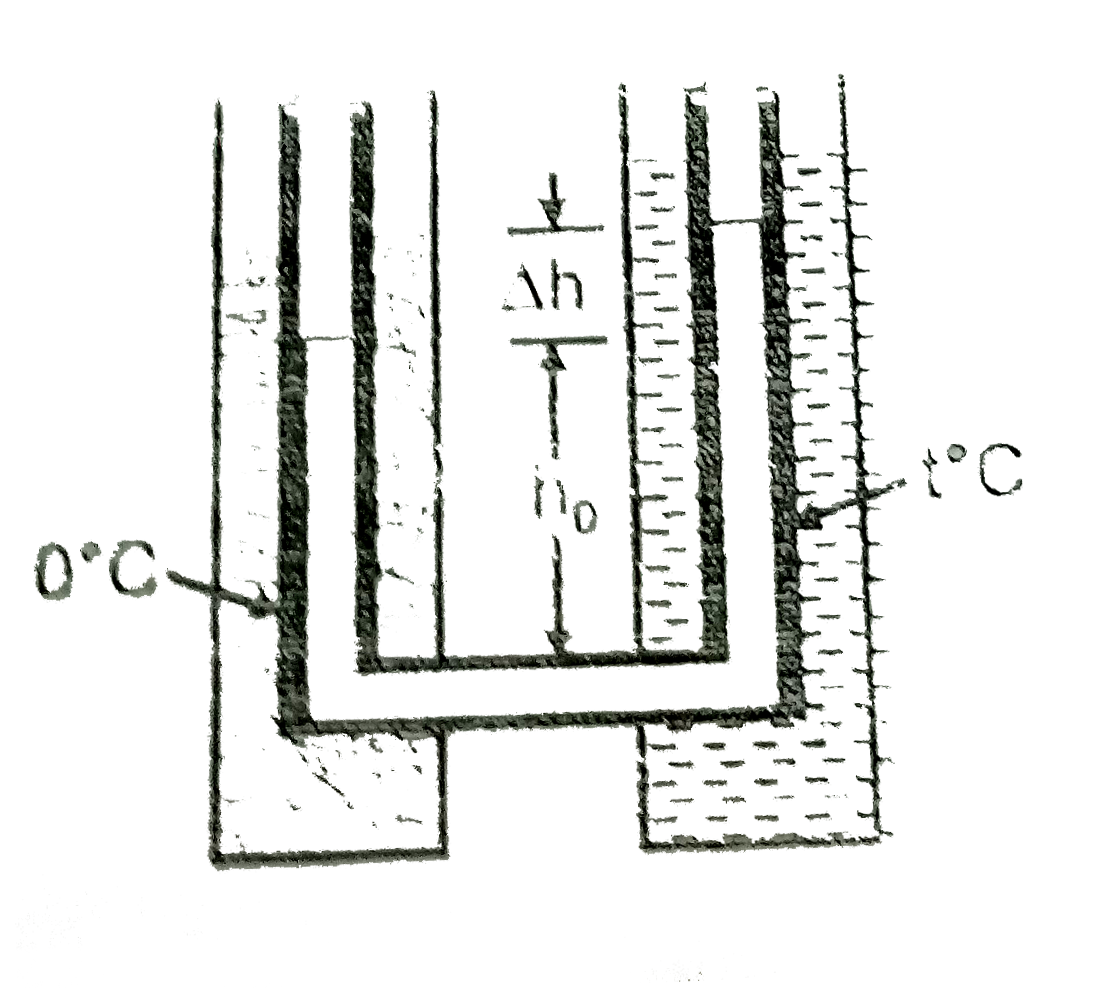
In figure shown, left arm of a U−tube is immersed in a hot water bath at temperature t∘C, and right arm is immersed in a bath of melting ice, the height of manometric liquid in respective column is h1 and h0. Determine the coefficient of expansion of the liquid.
_S01_006_Q01.png) View Solution
View SolutionA sinker of weight w0 ha an apparent weight w1 when weighed in a liquid at temperature t1 and w2 when weighed in the same liquid at temperature t2. The coefficient of cubical expansion of the material of the sinker is β. What is the coefficient of volume expansion of the liquid?
View Solution
Knowledge Check
- Question 1 - Select One
In a vertical U-tube containg a liquid, the two arms are maintained at different temperature, T1 and _(2), respectively. The liquid columns in the two arms have heights, l1 and l2, respectively. The coefficient of volume expansion of the liquid is equal to :
 Al2−l2l2T1−l1T2Bl1−l2l1T1−l2T2Cl1+l2l2T1+l1T2Dl1+l2l1T1+l2T2
Al2−l2l2T1−l1T2Bl1−l2l1T1−l2T2Cl1+l2l2T1+l1T2Dl1+l2l1T1+l2T2 - Question 2 - Select One
A solid whose volume does not change with temperature floats in a liquid. For two different temperatures t1 and t2 of the liqiud, fraction f1 and f2 of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
Af1−f2f2t1−f1t2Bf1−f2f1t1−f2t2Cf1+f2f2t1+f1t2Df1+f2f1t1+f2t2 - Question 3 - Select One
Two vertical glass tibes filled with a liquid are connected at their lower ends by a horizontal capillary tube. One tube is surrounded by a bath containing ice and water at 0∘C and the other by hot water a t∘C. The difference in the height of the liquid in the two columns is Δh, and the height of the colume at 0∘C is h0. coefficient of volume expansion of the liquid is.
 A(Δh).(h0t)B2Δhh0tC2h0ΔhtDh0Δht
A(Δh).(h0t)B2Δhh0tC2h0ΔhtDh0Δht
A sinker of weight w0 has an apparent weight w1 when weighed in a liquid at a temperature t1andw2 when weight in the same liquid at temperature t2. The coefficient of cubical expansion of the material of sinker is β. What is the coefficient of volume expansion of the liquid.
View SolutionThe ratio of coefficients of apparent expansions of the same liquid in two different vessels is 1:2. If α1 and α2 are the coefficient of linear expansions then coefficient of real expansion of the liquid is
View SolutionTwo rods having length l1andl2 made of materials with the linear expansion coefficient α1andα2 were soldered together. The equivalent coefficients of linear expansion for the obtained rod
View SolutionTwo rods of lengths L1 and L2 are welded together to make a composite rod of length (L1+L2). If the coefficient of linear expansion of the materials of the rod are α1 and α2 respectively. The effective coefficient of linear expansion of the composite rod is
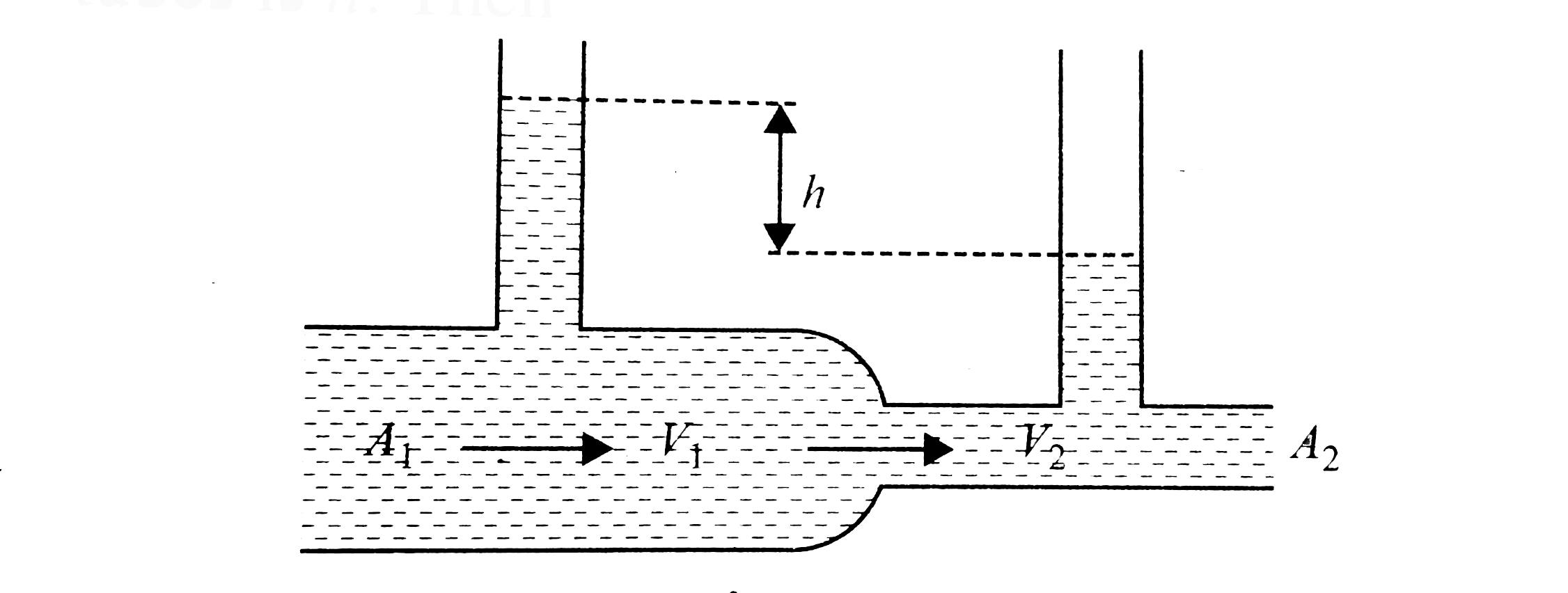
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 View Solution
View Solution

