Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. N⊙ofant(x) 0 1 2 3 4 5 TotalFrequency(f): 46 ? ? 25 10 5 200
To find the missing frequencies in the given frequency distribution, we will follow these steps:
Step 1: Set up the equations based on the given data
We know the following from the problem:
- The total frequency (Σf) = 200
- The mean (μ) = 1.46
The frequency distribution is as follows:
| No. of accidents (x) | Frequency (f) |
|-----------------------|---------------|
| 0 | 46 |
| 1 | x |
| 2 | y |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
Step 2: Write the equation for total frequency
From the total frequency, we can write:
46+x+y+25+10+5=200
This simplifies to:
x+y+86=200
So, we have:
x+y=200−86
x+y=114 (Equation 1)
Step 3: Write the equation for the mean
The formula for the mean is:
μ=Σ(xi⋅fi)Σfi
We need to calculate Σ(x_i * f_i):
- For x = 0: 0⋅46=0
- For x = 1: 1⋅x=x
- For x = 2: 2⋅y=2y
- For x = 3: 3⋅25=75
- For x = 4: 4⋅10=40
- For x = 5: 5⋅5=25
Now, summing these gives:
0+x+2y+75+40+25=x+2y+140
Setting this equal to the mean equation:
1.46=x+2y+140200
Step 4: Multiply through by 200 to eliminate the fraction
1.46⋅200=x+2y+140
Calculating 1.46⋅200:
292=x+2y+140
Rearranging gives:
x+2y=292−140
x+2y=152 (Equation 2)
Step 5: Solve the system of equations
Now we have two equations:
1. x+y=114 (Equation 1)
2. x+2y=152 (Equation 2)
We can solve these equations simultaneously.
From Equation 1, we can express x in terms of y:
x=114−y
Substituting this into Equation 2:
(114−y)+2y=152
This simplifies to:
114+y=152
So:
y=152−114
y=38
Now substitute y back into Equation 1 to find x:
x+38=114
x=114−38
x=76
Step 6: Conclusion
The missing frequencies are:
- Frequency for 1 accident (x) = 76
- Frequency for 2 accidents (y) = 38
- The mean (μ) = 1.46
|-----------------------|---------------|
| 0 | 46 |
| 1 | x |
| 2 | y |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
x+y=114 (Equation 1)
- For x = 1: 1⋅x=x
- For x = 2: 2⋅y=2y
- For x = 3: 3⋅25=75
- For x = 4: 4⋅10=40
- For x = 5: 5⋅5=25
x+2y=152 (Equation 2)
2. x+2y=152 (Equation 2)
y=38
x=114−38
x=76
- Frequency for 2 accidents (y) = 38
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the missing frequency in the following distribution, if it is known that the mean of the distribution is 50.16
 Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50. f=17,f1=32,f2=19 Total 120
View SolutionFind the mean of the followings frequency distribution :

View SolutionFind the mean for the following frequency distribution :
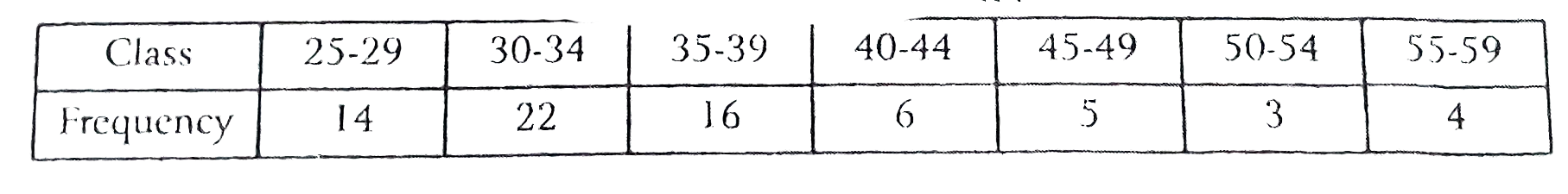
View SolutionFind the mean from the following frequency distribution:

View SolutionFind the mean and variance for the following frequency distributions in
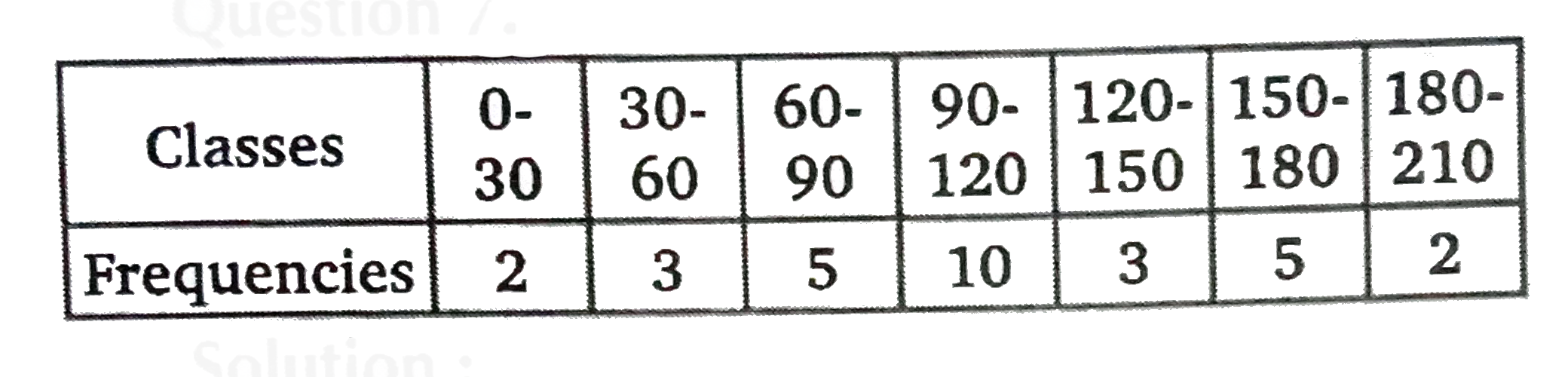
View SolutionFind the mean and variance for the following frequency distributions in
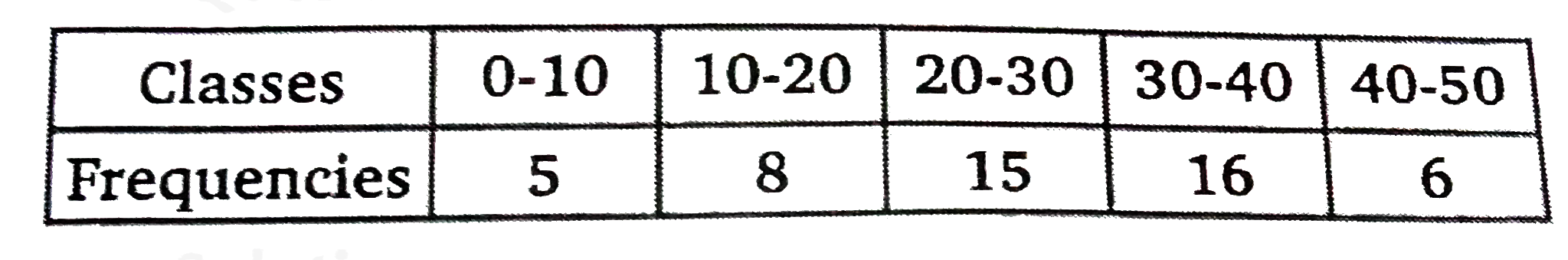
View SolutionFind the mean and variance for the following frequency distributions :

View Solution

