Gordon recently learned that his shadow is proportional to his height. He also learned that the shadows of other objects are proportional to their height. At three o'clock, his shadow measured 4 feet and the shadow of the tree in his front yard measured 18 feet. If Gordon is 6 feet tall, how tall is the tree ?
108 feet
72 feet
27 feet
24 feet
The correct Answer is:C
To solve the problem step by step, we will use the concept of proportionality between the height of an object and the length of its shadow.
1. Understanding Proportionality:
We know that the height of an object (h) is proportional to the length of its shadow (s). This can be expressed mathematically as:
h=k⋅s
where k is a constant of proportionality.
2. Finding the Constant of Proportionality:
For Gordon, we are given:
- Height hG=6 feet
- Shadow sG=4 feet
Plugging these values into the proportionality equation:
6=k⋅4
To find k, we rearrange the equation:
k=64=32
3. Setting Up the Equation for the Tree:
Now, we will use the same constant k to find the height of the tree. We know:
- Shadow of the tree sT=18 feet
We can express the height of the tree hT using the same proportionality constant:
hT=k⋅sT
Substituting the value of k and sT:
hT=32⋅18
4. Calculating the Height of the Tree:
Now we compute:
hT=3⋅182=542=27 feet
5. Conclusion:
Therefore, the height of the tree is 27 feet.
Final Answer:
The height of the tree is 27 feet.
We know that the height of an object (h) is proportional to the length of its shadow (s). This can be expressed mathematically as:
h=k⋅s
where k is a constant of proportionality.
For Gordon, we are given:
- Height hG=6 feet
- Shadow sG=4 feet
6=k⋅4
To find k, we rearrange the equation:
k=64=32
Now, we will use the same constant k to find the height of the tree. We know:
- Shadow of the tree sT=18 feet
hT=k⋅sT
Substituting the value of k and sT:
hT=32⋅18
Now we compute:
hT=3⋅182=542=27 feet
Therefore, the height of the tree is 27 feet.
The height of the tree is 27 feet.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - ELEMENTARY ALGEBRAEXERCISE - EXERCISE12videos
ELEMENTARY ALGEBRA
- BOOK - ENGLISH SATCHAPTER - DIAGNOSTIC TEST EXERCISE - MCQs (EXERCISE)50videos
DIAGNOSTIC TEST
- BOOK - ENGLISH SATCHAPTER - EXPONENTIAL AND LOGARITHMIC FUNCTIONS EXERCISE - Exercises10videos
EXPONENTIAL AND LOGARITHMIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
On level ground, a vertical rod 12 feet tall casis a shadow 4 feet long, and at the same time a nearby vertical flagpole casts a shadow 12 feet long. How many feet tall is the flagpole?
A4B8C12D36 - Question 2 - Select One
Jasper wants to measure the altiude of his kite . He ties the kite string to a spike driven into the ground and measures the angle between the string and the ground . Then he creates two similar triangles by adjusting the distance between an-8 foot pole and the spike until the angle created by a piece of string is the same as the angle he measured previously . the length of the string to the kite is 85 feet and the length of the string to the pole is 17 feet . which of the follpowing is closest to the height , in feet , that the kite is above the ground ?
 A25B40C102D110
A25B40C102D110 - Question 3 - Select One
A gardener is planting two types of trees. One type is seven feet tall and grows at a rate of 8 inches per year. The other type is four feet tall and its rate of the growth is 50% greater than the rate of the other tree. In how many years will the two grow to the same height?
A6B7C8D9
A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of (a) 15 ft/sec (b) 9 ft/sec (c) 6 ft/sec (d) none of these
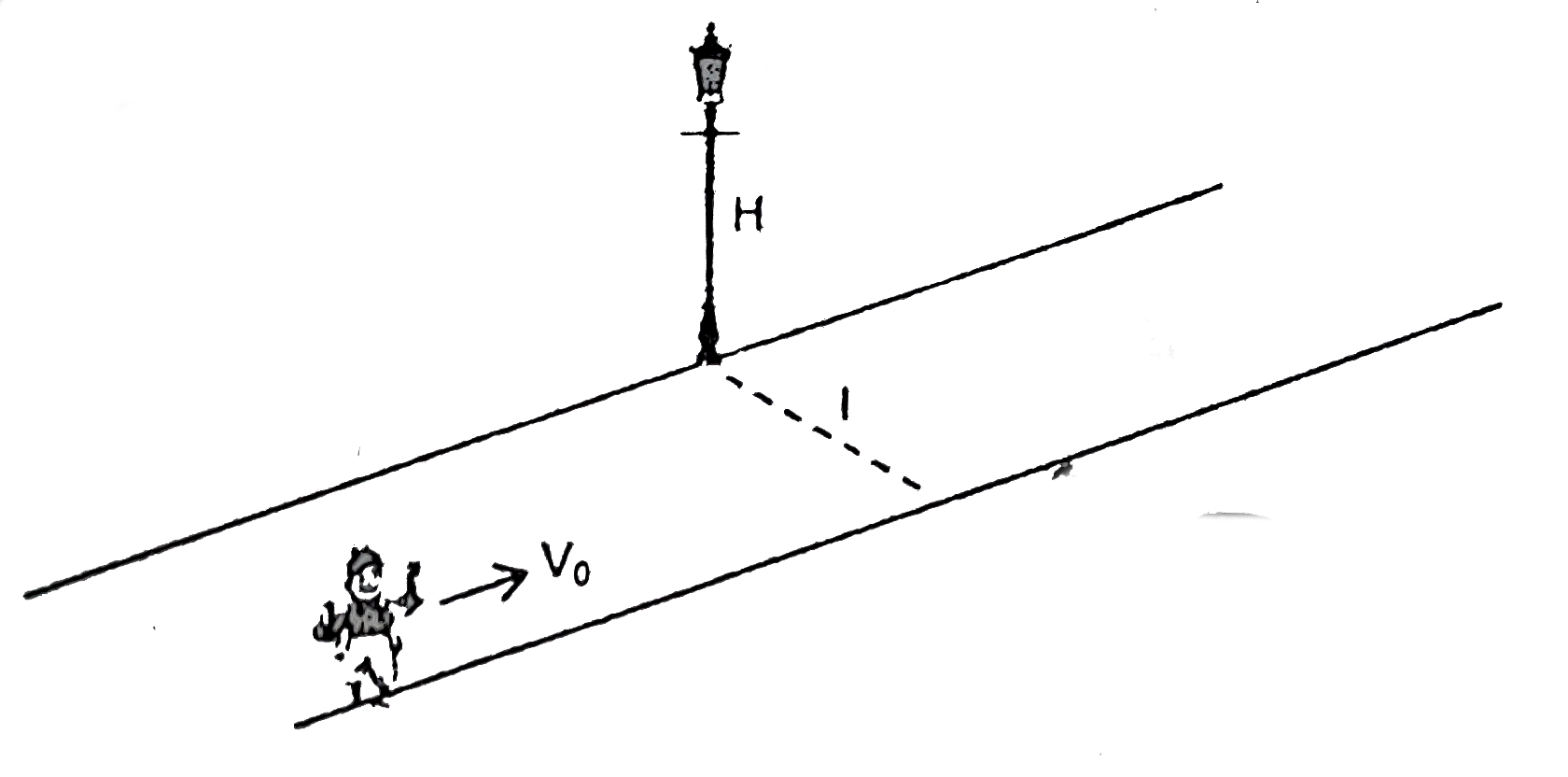
View SolutionA man of height h is walking at constant speed v0 along edge of a straight horizontal road. There is a lamp post of height H=2h on the other edge as shown. If speed of tip of shadow of his head is nv0 then find n.
 View Solution
View SolutionA man of height 1.7 m walks at a uniform speed of 6.6 m/min from a lamp post which is 5m high.Find the rate at which the length of his shadow increases.
View SolutionA man 160 cm tall, walks away from a source of light situated at the top of a pole 6m high at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 metre away from the pole.
View SolutionGary is using a 3D printer to create a miniature version of himself. The scale of the miniature is 0.4 inches to 1 foot oto Gary's actual height. If Gary is 5 feet and 9 inches tall, what will be the height of his 3D-Printed miniature? (12 inches=1 foot)
View Solution

