An angle in the standard (x,y) coordinate plane has its vertex at the origin and its initial side on the positive x-axis If the measure of an angle in standard position is (1,314∘), it has the same terminal side as an angle of each of the following measures EXCEPT:
594∘
314∘
234∘
−126∘
The correct Answer is:B
To solve the problem, we need to find which angle does not share the same terminal side as the angle of 1314∘. We can do this by reducing 1314∘ to an equivalent angle within the range of 0∘ to 360∘.
1. Find the equivalent angle of 1314∘ within 0∘ to 360∘:
- Since angles are periodic with a period of 360∘, we can subtract 360∘ repeatedly from 1314∘ until we get an angle within the desired range.
- First, subtract 360∘:
1314∘−360∘=954∘
- Subtract 360∘ again:
954∘−360∘=594∘
- Subtract 360∘ again:
594∘−360∘=234∘
- Now, 234∘ is within the range of 0∘ to 360∘.
2. List the angles to check against the options:
- The equivalent angle of 1314∘ is 234∘.
- Now we need to check the options given in the problem to see which angle does not share the same terminal side as 234∘.
3. Evaluate the options:
- Option 1: 594∘ (shares terminal side with 234∘)
- Option 2: 954∘ (shares terminal side with 234∘)
- Option 3: 234∘ (same angle)
- Option 4: −126∘ (find the equivalent positive angle)
- To convert −126∘ to a positive angle:
−126∘+360∘=234∘
- This also shares the same terminal side.
4. Identify the angle that does not share the terminal side:
- The only angle left to check is 314∘. We can check if it shares the same terminal side:
- Subtract 360∘ from 314∘:
314∘−360∘=−46∘
- The equivalent positive angle for −46∘ is:
−46∘+360∘=314∘
- Since 314∘ does not equal 234∘, it does not share the same terminal side.
Final Answer:
The angle that does not share the same terminal side as 1314∘ is 314∘.
- Since angles are periodic with a period of 360∘, we can subtract 360∘ repeatedly from 1314∘ until we get an angle within the desired range.
- First, subtract 360∘:
1314∘−360∘=954∘
- Subtract 360∘ again:
954∘−360∘=594∘
- Subtract 360∘ again:
594∘−360∘=234∘
- Now, 234∘ is within the range of 0∘ to 360∘.
- The equivalent angle of 1314∘ is 234∘.
- Now we need to check the options given in the problem to see which angle does not share the same terminal side as 234∘.
- Option 1: 594∘ (shares terminal side with 234∘)
- Option 2: 954∘ (shares terminal side with 234∘)
- Option 3: 234∘ (same angle)
- Option 4: −126∘ (find the equivalent positive angle)
- To convert −126∘ to a positive angle:
−126∘+360∘=234∘
- This also shares the same terminal side.
- The only angle left to check is 314∘. We can check if it shares the same terminal side:
- Subtract 360∘ from 314∘:
314∘−360∘=−46∘
- The equivalent positive angle for −46∘ is:
−46∘+360∘=314∘
- Since 314∘ does not equal 234∘, it does not share the same terminal side.
The angle that does not share the same terminal side as 1314∘ is 314∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the standard (x,y) coordinate plane below, an angle is shown whose vertex is the origin. One side of this angle with measure θ passes through (4, -3), and the other side include the positive x-axis. What is the cosine of θ?
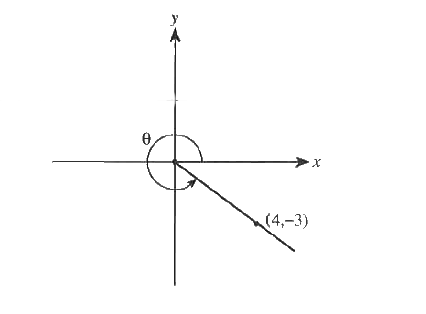 A−43B−34C−35D45
A−43B−34C−35D45ΔABC , shown below in the standard (x,y) coordinate plane is equilateral with vertex A at (0,w) and vertex B on the x- axis as shown . What are the coordinates of vertex C ?
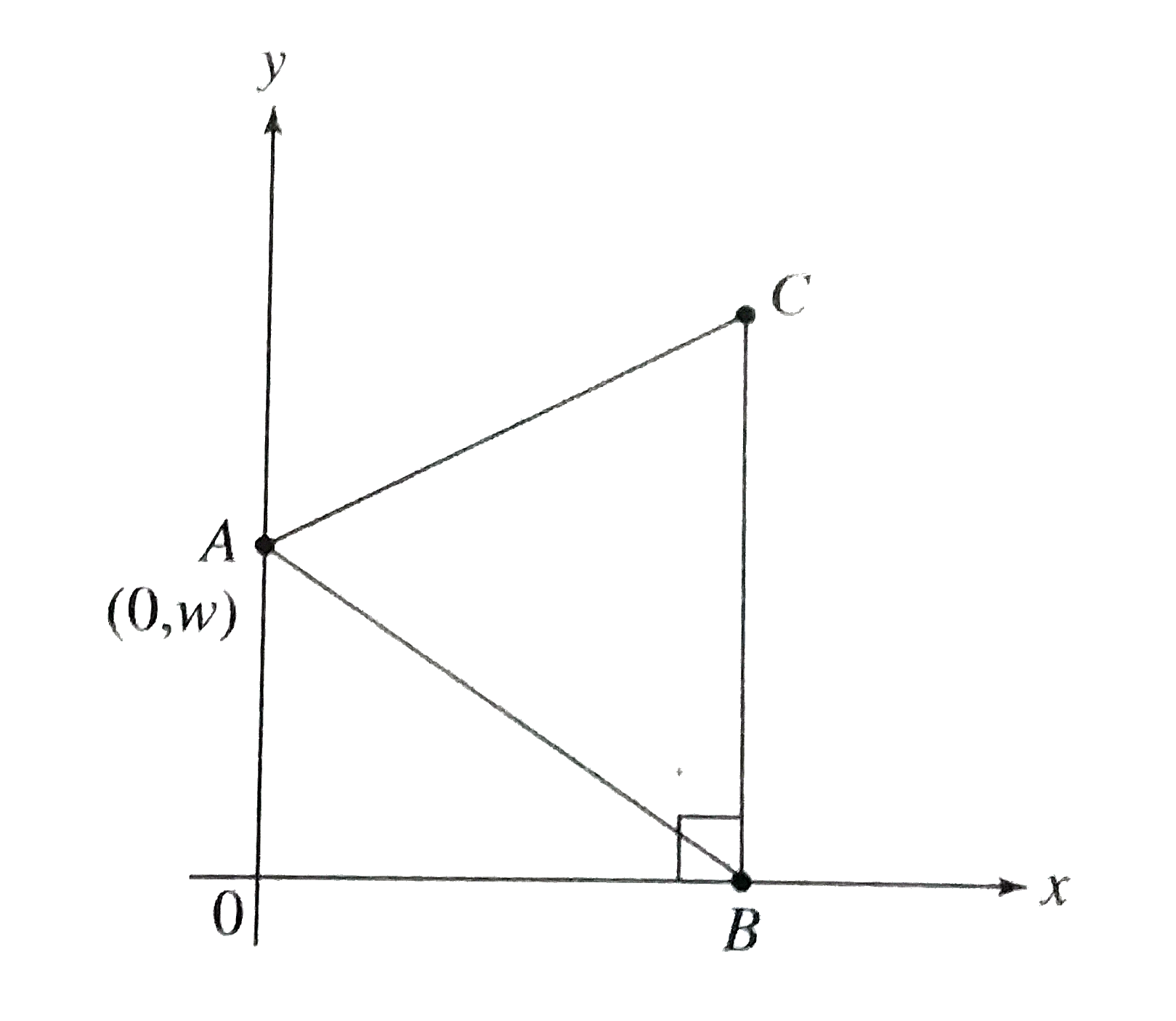 A(w,0)B(w,2w)C(w√3,w)D(w√3,2w)
A(w,0)B(w,2w)C(w√3,w)D(w√3,2w)Each of the following graphs in the standard (x,y) coordinate plane has the same scale on both axes. One graph is the graph of ax+by≤c, where 0<a<b<c. Which one is it?
A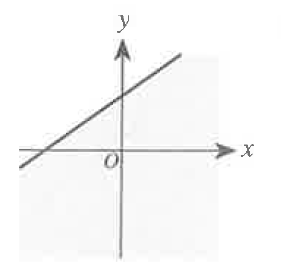 B
B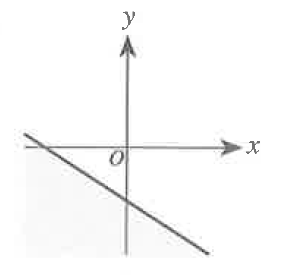 C
C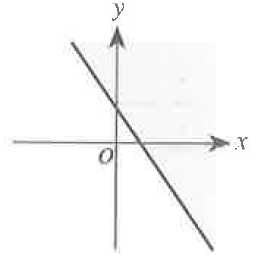 D
D
In x-y plane, a force 10N acts at an angle 30∘ to the positive direction of x-axis. The force can be written as
View SolutionA circle touches y-axis at (0, 2) and has an intercept of 4 units on the positive side of x-axis. The equation of the circle, is
View SolutionAn equilateral triangle has its circumcentre at origin and one of the sides is along the line x + y -1 = 0 and cordinate of vertex A is (-1,-1). Find the equations of the other two sides.
View SolutionA square of each side 2, lies above the x-axis and has one vertex at the origin. If one of the sides passing through the origin makes an angle 30∘ with the positive direction of the x-axis, then the sum of the x-coordinates of the vertices of the square is:
View SolutionA rectangle has one side on the positive y-axis and one side on the positive x -axis. The upper right hand vertex of the rectangle lies on the curve y=lnxx2. The maximum area of the rectangle is
View Solution