What is the largest value of m for which there exists a real value of n such that m2=196−n2?
14
95
182
196
The correct Answer is:A
To solve the problem, we need to find the largest value of m for which there exists a real value of n such that the equation m2=196−n2 holds true. We can follow these steps:
Step 1: Rewrite the equation
We start with the equation:
m2=196−n2
Rearranging this gives:
m2+n2=196
Step 2: Analyze the equation
This equation represents a circle with a radius of √196=14 in the m-n coordinate system. For n to be a real number, the expression 196−m2 must be non-negative.
Step 3: Set up the inequality
To ensure that n is real, we need:
196−m2≥0
This can be rearranged to:
m2≤196
Step 4: Solve for m
Taking the square root of both sides gives:
|m|≤14
This means:
−14≤m≤14
Step 5: Find the largest value of m
Since we are looking for the largest value of m, we take:
m=14
Conclusion
Thus, the largest value of m for which there exists a real value of n is:
14
---
We start with the equation:
m2=196−n2
Rearranging this gives:
m2+n2=196
This equation represents a circle with a radius of √196=14 in the m-n coordinate system. For n to be a real number, the expression 196−m2 must be non-negative.
To ensure that n is real, we need:
196−m2≥0
This can be rearranged to:
m2≤196
Taking the square root of both sides gives:
|m|≤14
This means:
−14≤m≤14
Since we are looking for the largest value of m, we take:
m=14
Thus, the largest value of m for which there exists a real value of n is:
14
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the lowest value of n that allows g orbitals to exist?
A6B7C4D5 - Question 2 - Select One
When the value of n = 2, m can have
A1 valueB3 valuesC4 valuesD7 values.
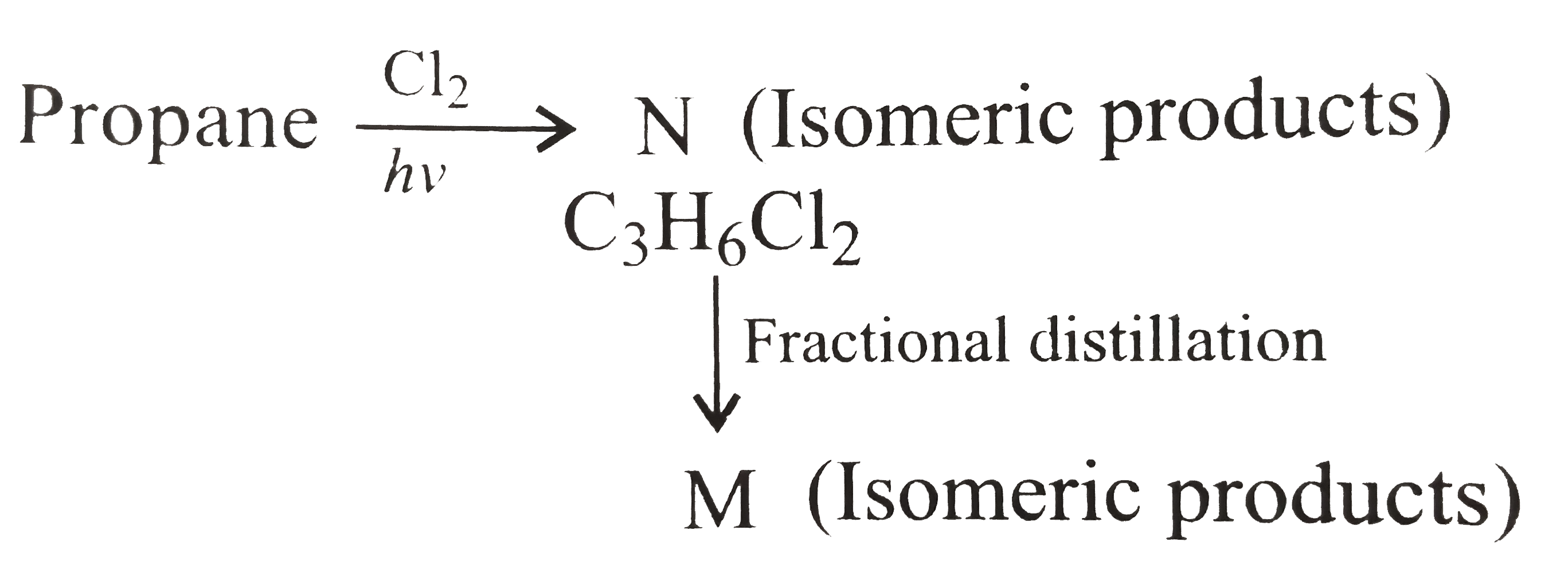
What are the numerical values of N and M?View Solution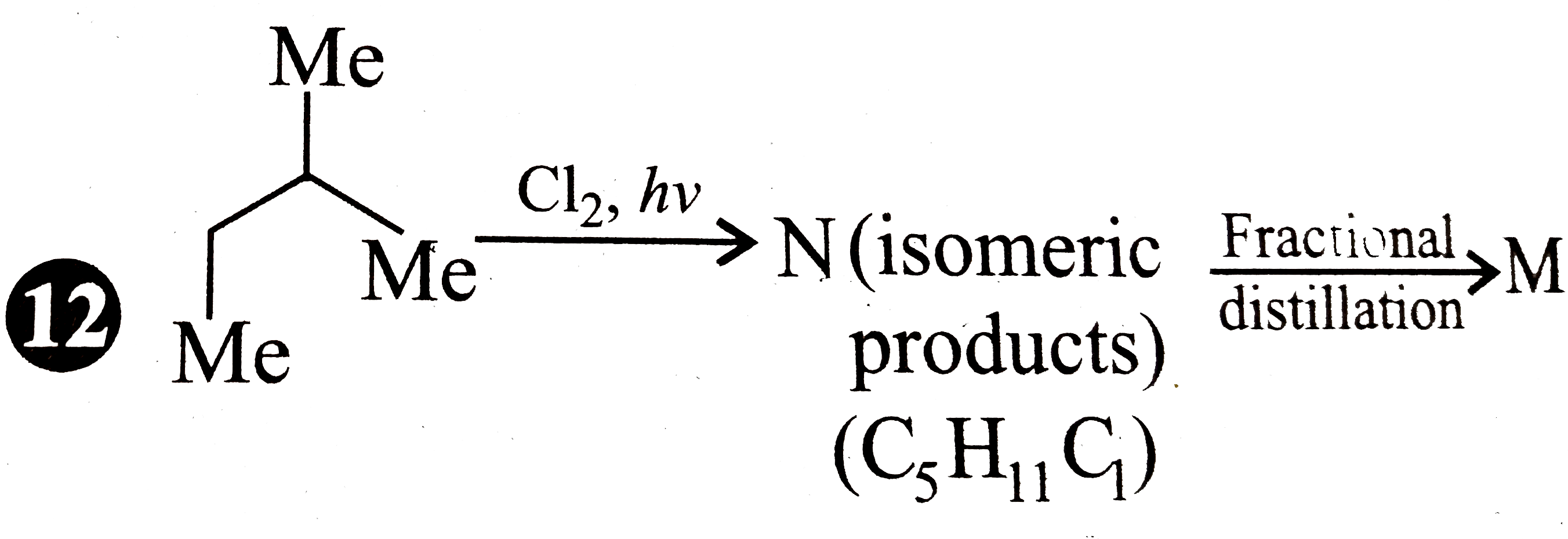
The value of N and M are:View Solution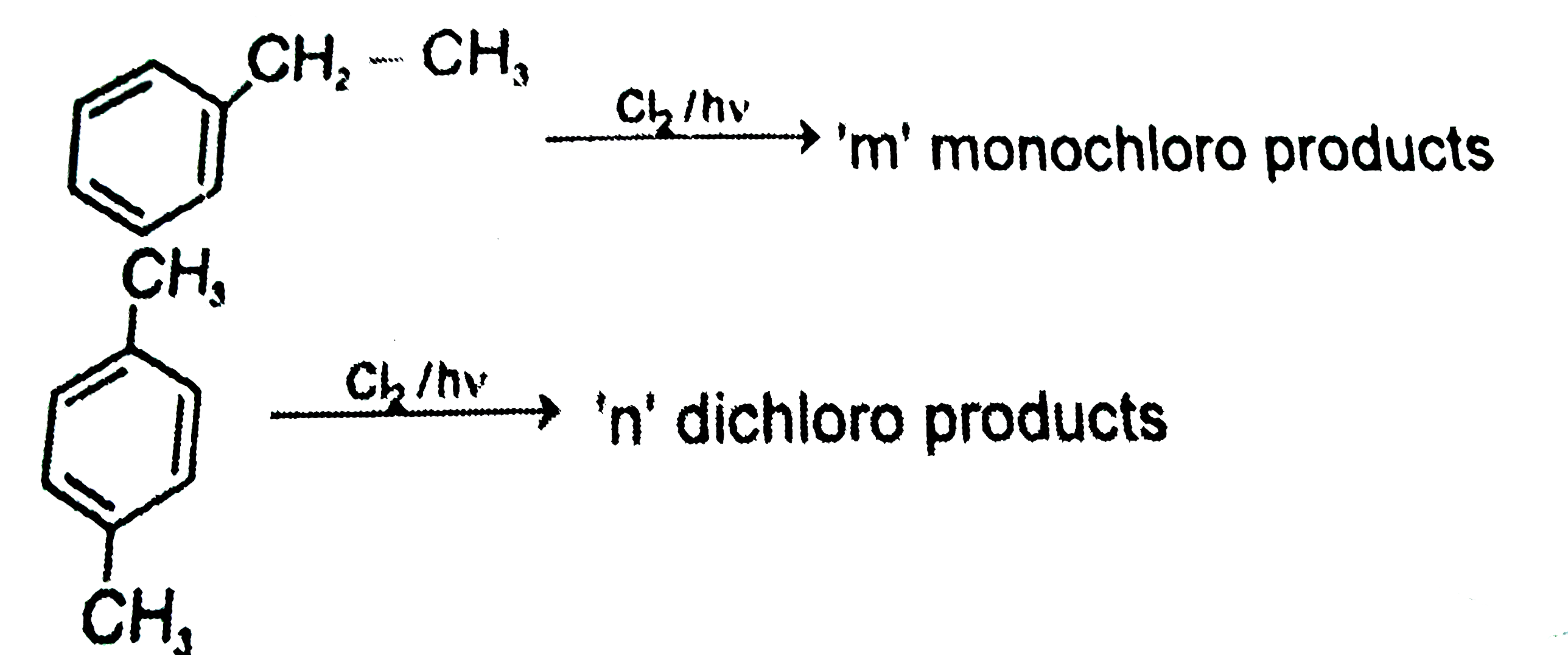
The value of m and n are respectively :View SolutionThe smallest positive integral value of n for which (1+√3i)n2 is real is
View Solution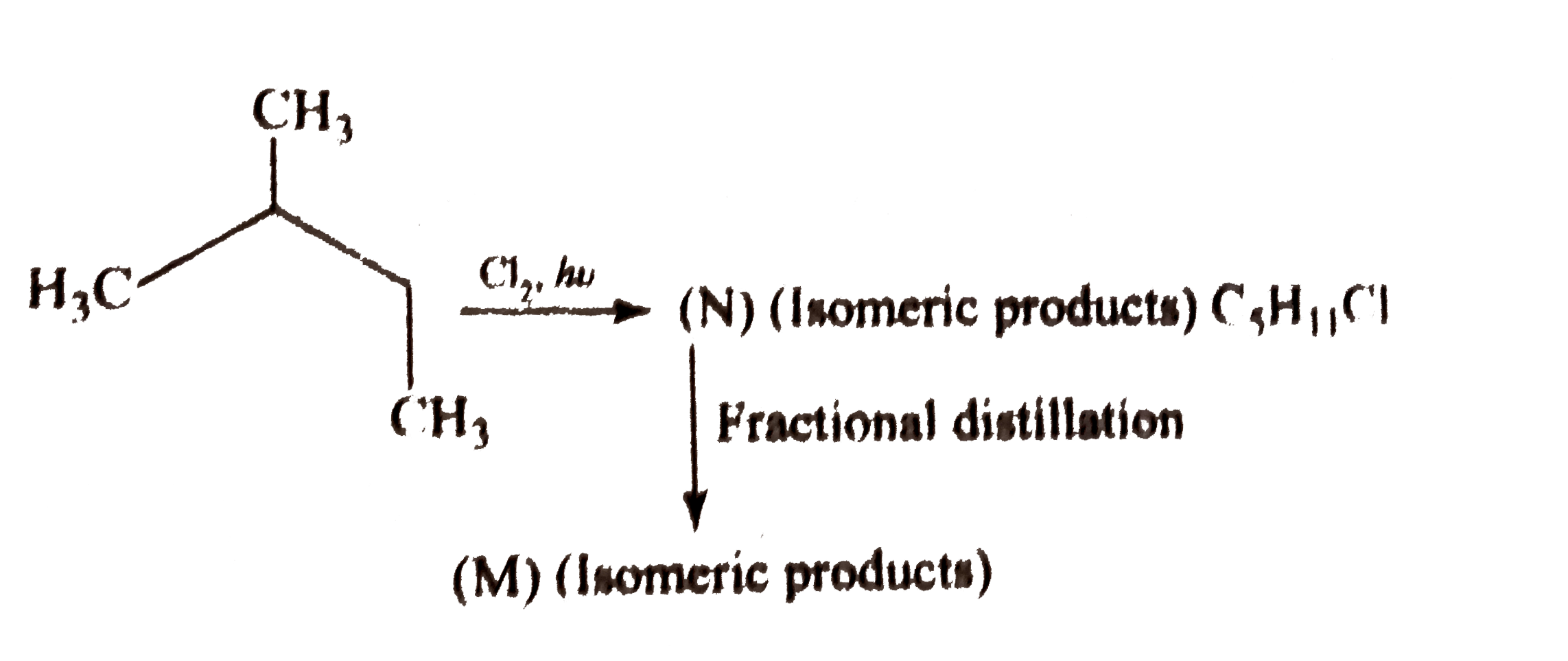
The numberical values of (N) and (M) are :View SolutionThe largest value of the positive integer k for which nk+1 divides 1+n+n2+....+n127, is
View Solution

