The 4 integers j,j,k and n have an average of 0. which of the following equations must be true ?
k=n
k=−j
k+n=−2j
k+n=0
The correct Answer is:C
To solve the problem, we need to find the relationship between the integers j,j,k, and n given that their average is 0.
1. Understanding the Average:
The average of the integers j,j,k, and n is given by the formula:
Average=Sum of valuesNumber of values
Here, the sum of the values is j+j+k+n and the number of values is 4.
2. Setting Up the Equation:
Since the average is given to be 0, we can set up the equation:
j+j+k+n4=0
3. Simplifying the Equation:
Multiply both sides of the equation by 4 to eliminate the denominator:
j+j+k+n=0
This simplifies to:
2j+k+n=0
4. Rearranging the Equation:
To find a relationship among j,k, and n, we can rearrange the equation:
k+n=−2j
5. Conclusion:
The equation k+n=−2j must be true given that the average of j,j,k, and n is 0.
Final Answer:
The equation that must be true is:
k+n=−2j
The average of the integers j,j,k, and n is given by the formula:
Average=Sum of valuesNumber of values
Here, the sum of the values is j+j+k+n and the number of values is 4.
Since the average is given to be 0, we can set up the equation:
j+j+k+n4=0
Multiply both sides of the equation by 4 to eliminate the denominator:
j+j+k+n=0
This simplifies to:
2j+k+n=0
To find a relationship among j,k, and n, we can rearrange the equation:
k+n=−2j
The equation k+n=−2j must be true given that the average of j,j,k, and n is 0.
The equation that must be true is:
k+n=−2j
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ab>0, then which one of the following must be true?
Aa/b>0Ba−b>0Ca+b>0Db−a>0If x is integer and x2 is even, which of the following must be true?
Ax is evenBx is oddCx3 is oddDx3 is evenIn the figure, line l and k are parallel. Which one of the following must be true?
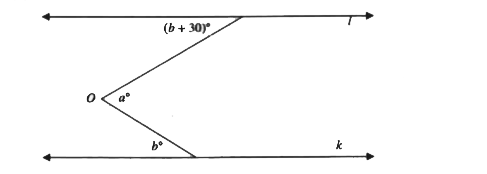 Aa lt bBa≤bCa=bDa>b
Aa lt bBa≤bCa=bDa>b
Which of the following statements is not true for J-shaped growth curve?
View SolutionLet m and n be 2 positive integers, such that m<n. Which of the following compound inequalities must be true?
View SolutionGiven that 2m+n2n=34, which of the following must also be true?
View SolutionWhen the integer n is divided by 2, the quotient is u and the remainder is 1. When the integer n is divided by 5, the quotient is v and the remainder is 3. Which one of the following must be true?
View SolutionIf k is a positive integer, which of the following represents the average of 3kand3k+2?
View Solution
