इस प्रश्न में प्रकथन 1 एवं प्रकथन 2 दिये गये हैं। प्रकथनों के पश्चात् दिये गये चार विकल्पों में से, उस विकल्प को चुनिए जोकि दोनों प्रकथनों का सर्वोत्तम वर्णन करता है। त्रिज्या R के एक रोधी ठोस गोले पर एकसमान धनात्मक आवेश घनत्व है। इस एकसमान आवेश वितरण के कारण विद्युत् विभव का मान गोले के केन्द्र पर, गोले के पृष्ठ पर और गोले से बाहर एक बिन्दु पर परिमित है। अनन्त पर विद्युत विभव का मान शून्य है-
प्रकथन 1. जब एक आवेश q को गोले के केन्द्र से पृष्ठ तक ले जाया जाता है, तब स्थितिज ऊर्जा में (prho)/(3 epsi_0) (pr)/(3epsi_0) है।
प्रकथन 1 गलत है, प्रकथन 2 सही है।
प्रकथन 1 सही है, प्रकथन 2 गलत है
प्रकथन 1 सही है, प्रकथन 2 सही है, प्रकथन 2 प्रकथन 1 की सही व्याख्या करता है
प्रकथन 1 सही है, प्रकथन 2 सही है, प्रकथन 2 प्रकथन 1 की सही व्याख्या नहीं करता है।
The correct Answer is:A
दिया गया कथन 1 विमीय रूप से गलत है।
गाउस के नियम से,
अतः कथन 2 सही है।
Topper's Solved these Questions
- विद्युत विभव Book:MITTAL PUBLICATIONChapter:विद्युत विभव Exercise:आंकिक प्रश्न
Explore 25 Videos
- विद्युत परिपथ Book:MITTAL PUBLICATIONChapter:विद्युत परिपथ Exercise:प्रतियोगी परीक्षा संबंधी प्रश्न ( बहुविकल्पीय प्रश्न)
Explore 20 Videos
- विधुत क्षेत्र Book:MITTAL PUBLICATIONChapter:विधुत क्षेत्र Exercise:प्रतियोगी परीक्षा सम्बन्धी प्रश्न
Explore 17 Videos
Similar Questions
एक इलेक्ट्रॉन 5×103 वोल्ट विभवान्तर से त्वरित किया जाता है। इसकी ऊर्जा वृद्धि की गणना जूल में कीजिए।
View Solutionएक मीटर ब्रिज से 90Ω के मानक प्रतिरोध के साथ एक प्रयोग करते समय, जब जॉकी को तार के बायें सिरे से 40.0 cm पर दबाया जाता है, तब मीटर ब्रिज में प्रयुक्त पैमाने का अल्पतमांक 1 mm है। अज्ञात प्रतिरोध का मान है -
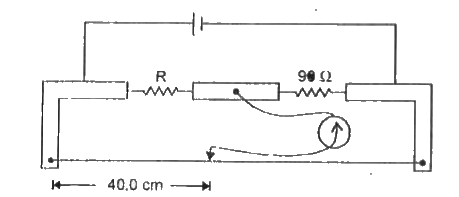
View Solutionएक आवेश Q वर्ग के प्रत्येक विपरीत कोने पर रखा है। एक आवेश q प्रत्येक अन्य दो कोनों पर रखा है। यदि Q पर नेट विधुत क्षेत्र शून्य बल हो तो Qq बराबर होगा।
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?
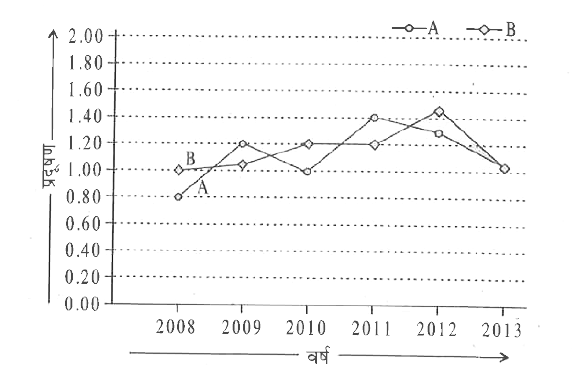
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?

View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionगोले एवं अर्ध गोले के आयतन से सम्बंधित प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|गोले के आयतन पर आधारित महत्वपूर्ण प्रश्न#!#अर्धगोले के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionकुचालक गोले के कारण वैधुत विभव
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#गोले का पृष्ठीय क्षेत्रफल#!#गोले का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View Solutionगोले के कारण विभव
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solution