The straight line y = -2x + 5 is best represented by :
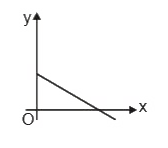
The correct Answer is:B
To solve the problem of identifying the representation of the straight line given by the equation y=−2x+5, we can follow these steps:
Step 1: Identify the slope and y-intercept
The equation of the line is in the slope-intercept form, which is given by:
y=mx+c
where m is the slope and c is the y-intercept.
From the equation y=−2x+5:
- The slope m=−2
- The y-intercept c=5
Step 2: Understand the implications of the slope and intercept
The slope m=−2 indicates that the line is decreasing. A negative slope means that as x increases, y decreases. The y-intercept c=5 indicates that the line crosses the y-axis at the point (0,5).
Step 3: Plot the y-intercept
To plot the line, we start by marking the y-intercept on the graph:
- At x=0, y=5. So, we plot the point (0,5).
Step 4: Find another point using the slope
Using the slope m=−2, we can find another point on the line. The slope can be interpreted as:
slope=ΔyΔx=−2
This means that for every increase of 1 in x, y decreases by 2.
Starting from the point (0,5):
- If x=1, then y=5−2(1)=3. So, we have another point (1,3).
Step 5: Plot the second point
Now, we plot the point (1,3) on the graph.
Step 6: Draw the line
Now that we have two points (0,5) and (1,3), we can draw a straight line through these points. This line represents the equation y=−2x+5.
Step 7: Analyze the graph
The graph will show a straight line that slopes downward from left to right, confirming that the slope is negative. The line crosses the y-axis at (0,5).
Conclusion
The straight line represented by the equation y=−2x+5 is a line with a negative slope that intersects the y-axis at 5.
---
The equation of the line is in the slope-intercept form, which is given by:
y=mx+c
where m is the slope and c is the y-intercept.
- The slope m=−2
- The y-intercept c=5
The slope m=−2 indicates that the line is decreasing. A negative slope means that as x increases, y decreases. The y-intercept c=5 indicates that the line crosses the y-axis at the point (0,5).
To plot the line, we start by marking the y-intercept on the graph:
- At x=0, y=5. So, we plot the point (0,5).
Using the slope m=−2, we can find another point on the line. The slope can be interpreted as:
slope=ΔyΔx=−2
This means that for every increase of 1 in x, y decreases by 2.
- If x=1, then y=5−2(1)=3. So, we have another point (1,3).
Now, we plot the point (1,3) on the graph.
Now that we have two points (0,5) and (1,3), we can draw a straight line through these points. This line represents the equation y=−2x+5.
The graph will show a straight line that slopes downward from left to right, confirming that the slope is negative. The line crosses the y-axis at (0,5).
The straight line represented by the equation y=−2x+5 is a line with a negative slope that intersects the y-axis at 5.
Similar Questions
Knowledge Check
Two straight line paths are represented by the equation 2x−y=2 and −4x+2y=6. Then the paths will
Across each other at one pointBnot cross each otherCcross each other at two pointsDcross each other at infinitely many pointsTwo straight line paths are represented by the equations 2x -y = 2 and -4x + 2y = 6 . Then , the paths will
ACross each other at one pointBNot cross each otherCCross each other at two pointsDCross each other at infinitely many pointsThe straight lines 5x + 4y = 0, x + 2y - 10 = 0 and 2x + y + 5 = 0 are
AconcurrentBthe sides of an equilateral triangleCthe sides of a right angled triangleDNone of the above
The angle between the straight lines represented by (x2+y2)sin2α=(xcosα−ysinα)2 is
View SolutionThe nature of straight lines represented by the equation 4x2+12xy+9y2=0 is
View SolutionThe straight lines represented by the equation 9x2−12xy+4y2=0 are
View SolutionTo which of the following types the straight lines represented by 2x+3y−7=0and2x+3y−5=0 belong
View SolutionIf the angle between the straight lines represented by 2x2+5xy+3y2+7y+4=0 is tan−1m then [1πm] is (where [.] denote greatest integer function)
View Solution
