A particle falls from a height h and rebounds to a height h1(h1<h), then which of the graph represents the motion correct ?
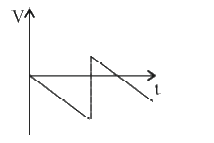
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle that falls from a height h and rebounds to a height h1 (where h1<h). We will describe the motion in terms of velocity and time, and then determine the correct graph that represents this motion.
1. Understanding the Motion:
- The particle falls from a height h under the influence of gravity. As it falls, its velocity increases due to gravitational acceleration.
- Upon reaching the ground, it collides with the ground and rebounds to a height h1, which is less than h.
2. Velocity During Free Fall:
- As the particle falls, its velocity increases. If we take the downward direction as negative, the velocity just before hitting the ground can be calculated using the equation:
v=√2gh
- At the moment just before impact, the velocity is at its maximum and directed downwards (negative).
3. Impact and Rebound:
- Upon hitting the ground, the particle's velocity direction changes from negative to positive. This is an instantaneous change in direction.
- After the impact, the particle moves upwards, and its velocity decreases as it rises until it reaches the maximum height h1 where the velocity becomes zero.
4. Velocity During Ascent:
- As the particle ascends, it decelerates due to gravity until it reaches the height h1. The velocity decreases from a positive value to zero at the peak of the rebound.
5. Graph Representation:
- The graph of velocity versus time will show:
- A negative slope as the particle falls (increasing negative velocity).
- A sudden change in direction at the point of impact (from negative to positive).
- A positive slope as the particle rises (decreasing positive velocity until it reaches zero).
Conclusion:
The correct graph will show a continuous increase in negative velocity as the particle falls, a sudden change to positive velocity at the point of impact, and a gradual decrease in positive velocity as the particle rises until it reaches the height h1.
- The particle falls from a height h under the influence of gravity. As it falls, its velocity increases due to gravitational acceleration.
- Upon reaching the ground, it collides with the ground and rebounds to a height h1, which is less than h.
- As the particle falls, its velocity increases. If we take the downward direction as negative, the velocity just before hitting the ground can be calculated using the equation:
v=√2gh
- At the moment just before impact, the velocity is at its maximum and directed downwards (negative).
- Upon hitting the ground, the particle's velocity direction changes from negative to positive. This is an instantaneous change in direction.
- After the impact, the particle moves upwards, and its velocity decreases as it rises until it reaches the maximum height h1 where the velocity becomes zero.
- As the particle ascends, it decelerates due to gravity until it reaches the height h1. The velocity decreases from a positive value to zero at the peak of the rebound.
- The graph of velocity versus time will show:
- A negative slope as the particle falls (increasing negative velocity).
- A sudden change in direction at the point of impact (from negative to positive).
- A positive slope as the particle rises (decreasing positive velocity until it reaches zero).
The correct graph will show a continuous increase in negative velocity as the particle falls, a sudden change to positive velocity at the point of impact, and a gradual decrease in positive velocity as the particle rises until it reaches the height h1.
Similar Questions
Two steel balls fall freely on an elastic slab. The first ball is dropped from a height h1 and the second from a height h2(h2<h1)sec after the first ball. After the passage of time T, the velocities of the balls coincide in magnitude and direction. Determine the time T and the time interval during which the velocities of the two balls will be equal assuming that the balls do not collide.
View SolutionA particle falls from a height h, upon a fixed horizontal plane. If e be the coefficient of restitution, the whole time taken before the particle has finished rebounding is √(2hg)1+e1−e
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m falls from a height h on a mass m and gets stuck to it. Then,
 Aacceleration of the pulley - mass system after impact is given by g/5.Bthe height to which 3m mass rises is h/5Cthe height to which 3m mass rises is h/3Dacceleration of the pulley mass system after impact is g/3
Aacceleration of the pulley - mass system after impact is given by g/5.Bthe height to which 3m mass rises is h/5Cthe height to which 3m mass rises is h/3Dacceleration of the pulley mass system after impact is g/3 - Question 2 - Select One
A ball released from a height ho above a horizontal surface rebounds to a height h1, after one bounce. The graph that relates h0 to h1 is shown Fig. If the ball (of the mass m) was dropped from an initial height h and made three bounces, the kinetic energy of the ball immediately after the third impact with the surface was
 A(0.8)3mghB(0.8)2mghC0.8mg(h/3)D[1−(0.8)3]mgh
A(0.8)3mghB(0.8)2mghC0.8mg(h/3)D[1−(0.8)3]mgh - Question 3 - Select One
A ball of mass m falls vertically to the ground from a height h1 and rebound to a height h1 and rebound to a height h2. The change in momentum of the ball on striking the ground is.
Amg(h1−h2)Bm(√2gh1+√2gh2)Cm√2g(h1+h2)Dm√2g(h1+h2)
A ball of mass m falls vertically to the ground from a height h1 and rebound to a height h2. The change in momentum of the ball on striking the ground is.
View SolutionA body is allowed to fall on the ground from a height h1. If it is rebound to a height h2 then the coefficient of restitution is:
View SolutionA ball falls from rest from a height h onto a floor, and rebounds to a height h/4. The coefficient of restitution between the ball and the floor is
View SolutionA particle falls from a height h on a fixed horizontal plate and rebounds. If e is the coefficient of restitution, the total distance travelled by the particle before it stops rebounding is
View SolutionA particle falls from a height h upon a fixed horizontal plane and rebounds. If e is the coefficient of restitution, the total distance travelled before rebounding has stopped is :
View Solution

