A ball after falling a distance of 5 meter rest hits elastically the floor of a lift and rebounds. At the time of impact the lift was moving up with a velocity of 1m/sec. The velocity with which the ball rebounds just after impact is : (g=10m/sec2)
10 m/sec
11m/sec
12m/sec
13m/sec
The correct Answer is:C
To solve the problem, we need to find the velocity with which the ball rebounds just after hitting the floor of the lift. We will use the principles of conservation of momentum and the concept of elastic collisions.
1. Determine the velocity of the ball just before impact:
The ball falls from a height of 5 meters. We can use the equation of motion to find the velocity just before it hits the ground:
v2=u2+2gh
where:
- u=0 (initial velocity when dropped)
- g=10m/s2 (acceleration due to gravity)
- h=5m (height fallen)
Substituting the values:
v2=0+2×10×5=100
v=√100=10m/s
2. Consider the velocity of the lift:
At the moment of impact, the lift is moving upwards with a velocity of 1m/s.
3. Determine the relative velocities:
The velocity of the ball just before impact is 10m/s downwards, and the lift is moving upwards at 1m/s. Therefore, the relative velocity of approach (the velocity of the ball towards the lift) is:
vapproach=v+vlift=10+1=11m/s
4. Apply the coefficient of restitution:
Since the collision is elastic, the coefficient of restitution e=1. The velocity of separation after the collision can be expressed as:
vseparation=e×vapproach=1×11=11m/s
5. Determine the velocity of the ball after impact:
The ball rebounds upwards after the collision. The velocity of the ball after impact v′ can be calculated as:
v′=vlift+vseparation=1+11=12m/s
Thus, the velocity with which the ball rebounds just after impact is 12 m/s upwards.
The ball falls from a height of 5 meters. We can use the equation of motion to find the velocity just before it hits the ground:
v2=u2+2gh
where:
- u=0 (initial velocity when dropped)
- g=10m/s2 (acceleration due to gravity)
- h=5m (height fallen)
v2=0+2×10×5=100
v=√100=10m/s
At the moment of impact, the lift is moving upwards with a velocity of 1m/s.
The velocity of the ball just before impact is 10m/s downwards, and the lift is moving upwards at 1m/s. Therefore, the relative velocity of approach (the velocity of the ball towards the lift) is:
vapproach=v+vlift=10+1=11m/s
Since the collision is elastic, the coefficient of restitution e=1. The velocity of separation after the collision can be expressed as:
vseparation=e×vapproach=1×11=11m/s
The ball rebounds upwards after the collision. The velocity of the ball after impact v′ can be calculated as:
v′=vlift+vseparation=1+11=12m/s
Similar Questions
A small ball falling vertically downward with constant velocity 2m/s strikes elastically an inclined plane moving with velocity 2m/s as shown in figure. The velocity of rebound of the ball with respect ground is

View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View Solution
Knowledge Check
A ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
A11 m/sB12 m/sC13 m/sD9 m/sA ball falls from a height of 5 m and strikes a lift which is moving in the upward direction with a velocity of 1ms−1, then the velocity with which the ball rebounds after collision will be
A11ms−1 downwardsB12ms−1 upwardsC13ms−1 upwardsD12ms−1 downwardsA ball is dropped from a height h on a horizontal plane and the coefficient of restitution for the impact is e, the velocity with which the ball rebounds from the flor is
AehBeghCe√(gh)De√(2gh)
A ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball is dropped from a height of 20m and rebounds with a velocity which is 34 of the velocity with which it hits the ground. What is the time interval between the first and second bunces (g=10m/s2)
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
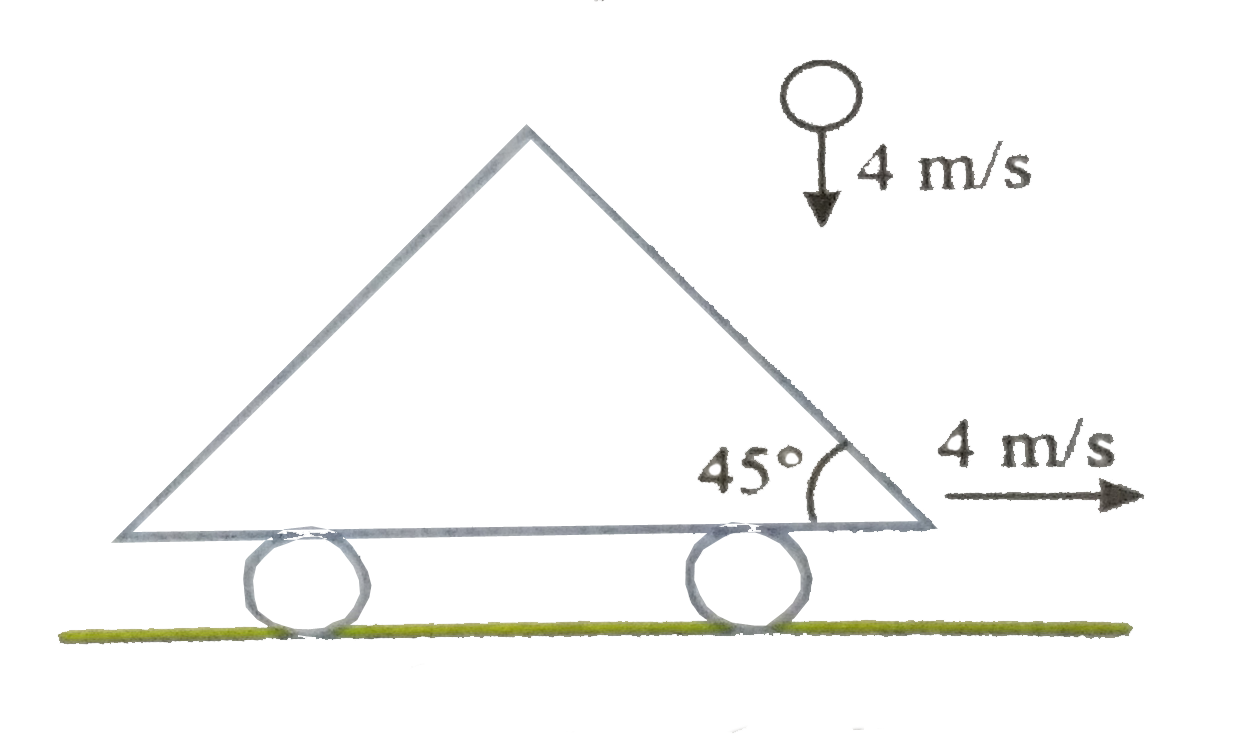
View SolutionA ball of mass 1 kg. moving with velocity 7 m/sec overtakes and collides with a ball of mass 2 kg. moving with velocity 1 m/sec in the same direction. If e = 3 / 4, the velocity of the lighter ball after impact is
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View Solution
