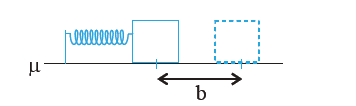
For the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :
μmgK
2μmgK
μgK
Kμmg
The correct Answer is:B
Step by step video & image solution for For the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
View SolutionIn the string mass system shown in the figure, the string is compressed by x0=mg2k from its natural length and block is relased from rest. Find the speed o the block when it passes through P (mg/4k distance from mean position)
_S01_030_Q01.png)
View Solution
Knowledge Check
A mass-spring system oscillates such that the mass moves on a rough surface having coefficient of friction μ. It is compressed by a distance a from its normal length and, on being released, it moves to a distance b from its equilibrium position. The decrease in anplitude for one half-cycle (-a to b) is
AμmgkB2μmgkCμgkDkμmgThe system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.
Athe particles perform SHM with time period π10secBthe block of mass 3 kg perform SHM with amplitude 4 cmCthe block of mass 6 kg will have maximum momentum 2.40kgm/sDnone of theseA spring of force constant K is first stretched by distance a from its natural length and then further by distance b. The work done in stretching the part b is
A12Ka(a−b)B12Ka(a+b)C12Kb(a−b)D12Kb(2a+b)
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
View SolutionA block of mass m=0.1kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View SolutionThe ration of kinetic energy to the potential energy of a particle executing SHM at a distance equal to half its amplitude , the distance being measured from its equilibrium position is
View Solution