Four masses 1, 2, 3 and 4 kg each are placed on four corners A, B, C and D of a square of side m. The moment of inertia of this system about an axis passing through the point of inter-section of diagonals and perpendicular to the plane of the square will be:
The correct Answer is:C
To find the moment of inertia of the system about an axis passing through the intersection of the diagonals of the square and perpendicular to the plane of the square, we can follow these steps:
Step 1: Understand the Configuration
We have a square ABCD with masses placed at its corners:
- Mass at A (1 kg)
- Mass at B (2 kg)
- Mass at C (3 kg)
- Mass at D (4 kg)
The side length of the square is given as √2 m.
Step 2: Determine the Coordinates of the Masses
We can place the square in a coordinate system:
- A (0, 0)
- B (√2, 0)
- C (√2, √2)
- D (0, √2)
The point of intersection of the diagonals (the center of the square) is at:
- O (√22,√22)
Step 3: Calculate the Distance from the Center to Each Mass
The distance r from the center O to each mass is calculated as follows:
1. For mass at A (1 kg):
rA=
⎷(0−√22)2+(0−√22)2=√24+24=√1=1 m
2. For mass at B (2 kg):
rB=
⎷(√2−√22)2+(0−√22)2=
⎷(√22)2+(−√22)2=√1=1 m
3. For mass at C (3 kg):
rC=
⎷(√2−√22)2+(√2−√22)2=
⎷(√22)2+(√22)2=√1=1 m
4. For mass at D (4 kg):
rD=
⎷(0−√22)2+(√2−√22)2=
⎷(−√22)2+(√22)2=√1=1 m
Step 4: Calculate the Moment of Inertia
The moment of inertia I is given by the formula:
I=∑mir2i
Where mi is the mass and ri is the distance from the axis of rotation.
Calculating for each mass:
- For mass at A:
IA=1⋅(12)=1 kg m2
- For mass at B:
IB=2⋅(12)=2 kg m2
- For mass at C:
IC=3⋅(12)=3 kg m2
- For mass at D:
ID=4⋅(12)=4 kg m2
Now, summing these contributions:
I=IA+IB+IC+ID=1+2+3+4=10 kg m2
Final Answer
The moment of inertia of the system about the specified axis is 10 kg m2.
---
We have a square ABCD with masses placed at its corners:
- Mass at A (1 kg)
- Mass at B (2 kg)
- Mass at C (3 kg)
- Mass at D (4 kg)
We can place the square in a coordinate system:
- A (0, 0)
- B (√2, 0)
- C (√2, √2)
- D (0, √2)
- O (√22,√22)
The distance r from the center O to each mass is calculated as follows:
rA=
⎷(0−√22)2+(0−√22)2=√24+24=√1=1 m
rB=
⎷(√2−√22)2+(0−√22)2=
⎷(√22)2+(−√22)2=√1=1 m
rC=
⎷(√2−√22)2+(√2−√22)2=
⎷(√22)2+(√22)2=√1=1 m
rD=
⎷(0−√22)2+(√2−√22)2=
⎷(−√22)2+(√22)2=√1=1 m
The moment of inertia I is given by the formula:
I=∑mir2i
Where mi is the mass and ri is the distance from the axis of rotation.
- For mass at A:
IA=1⋅(12)=1 kg m2
- For mass at B:
IB=2⋅(12)=2 kg m2
- For mass at C:
IC=3⋅(12)=3 kg m2
- For mass at D:
ID=4⋅(12)=4 kg m2
I=IA+IB+IC+ID=1+2+3+4=10 kg m2
The moment of inertia of the system about the specified axis is 10 kg m2.
Similar Questions
Four particles of masses 4kg,2kg,3kgand5kg are respectively located at the four corners A,B,C,D of a square of side 1m. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicualr to the plane of the square. (ii) side AB (ii) diagonal BD.
View SolutionFour point masses of 5 g each are placed at the four corners fo a square of side 10 cm. Find the moment of inertia of the system (i) about an axis coinciding with one of the sides and (ii) about an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square.
View Solution
Knowledge Check
Four point masses, each of value m, are placed at the corners of square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is -
A2ml2B√3ml2C3ml2Dml2Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A3ml2Bml2C2ml2D√3ml2Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A√3ml2B3ml2Cml2D2ml2
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionMoment of inertia of a square plate of side l about the axis passing through one of the corner and perpendicular to the plane of square plate is given by :
View SolutionFour point masses, each of value m, are placed at the corners of a squre ABCD of side l. The moment of inertia of the is system about an axis passing through A and parallel to BD is
View SolutionFour point masses each of value m, are placed at the corners of a square ABCD of side l, The moment of inertia of the system about an axis passing throught A and parallel to BD is
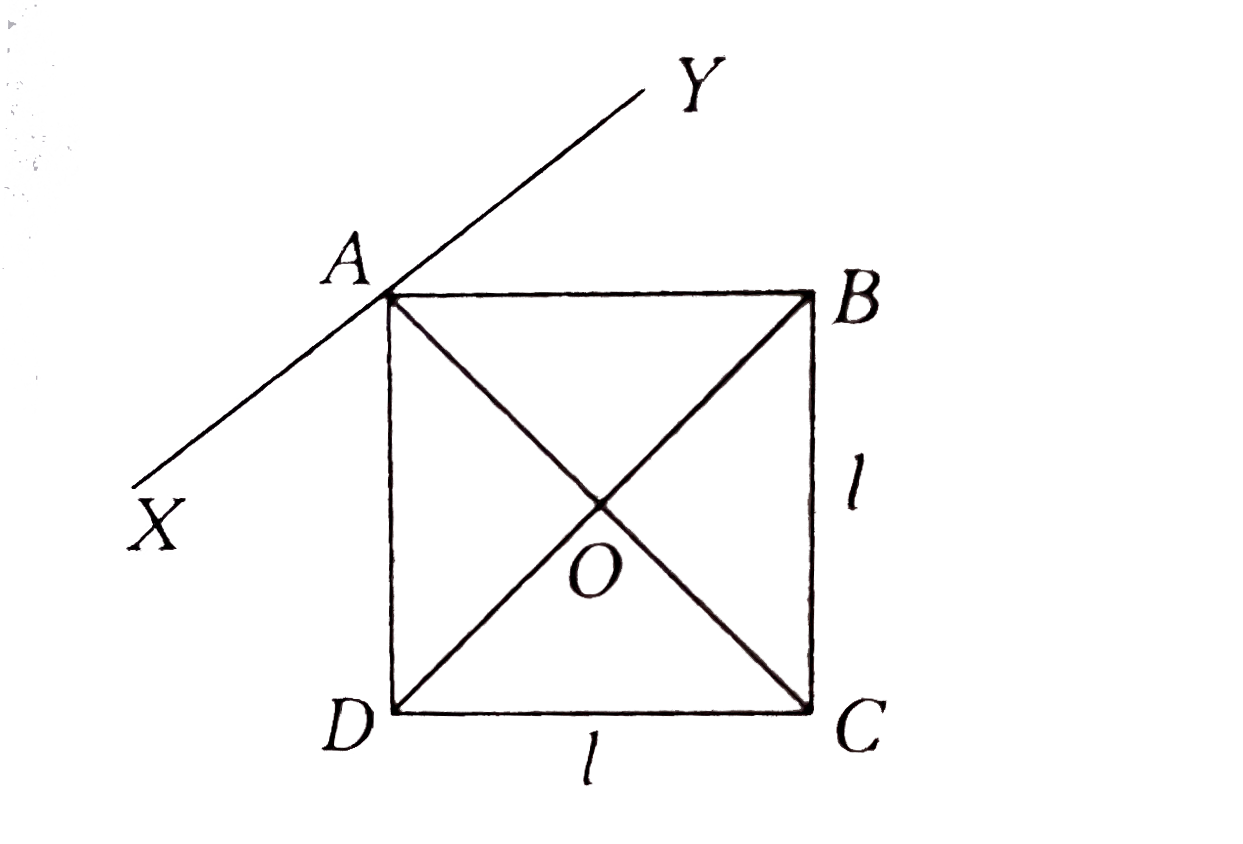
View SolutionFour bodies of masses 2, 3, 5 and 8 kg are placed at the four corners of a square of side 2 m. The position of CM will be -
View Solution
