The M.I. of a thin rod of length 1 about the perpendicular axis through its centre is I. The M.I. of square structure made by four such rods a perpendicular axis to the plane and through the centre will be:
4I
8I
12I
16I
The correct Answer is:D
To solve the problem, we need to find the moment of inertia (M.I.) of a square structure made by four thin rods, each of length 1 meter, about a perpendicular axis through the center of the square.
1. Understand the Moment of Inertia of a Single Rod:
The moment of inertia I of a thin rod of length L about an axis perpendicular to its length and through its center is given by the formula:
I=mL212
Here, L=1 meter, so we can denote the moment of inertia of one rod as:
I=m(12)12=m12
2. Determine the Configuration of the Square:
When we arrange four such rods to form a square, each rod will be positioned at the sides of the square. The length of each side of the square is 1 meter.
3. Calculate the Moment of Inertia about the Center:
To find the moment of inertia of the square structure about an axis perpendicular to the plane of the square and through its center, we can use the perpendicular axis theorem. According to this theorem:
Iz=Ix+Iy
where Iz is the moment of inertia about the perpendicular axis, and Ix and Iy are the moments of inertia about the two axes in the plane of the square.
4. Calculate Ix and Iy:
Each side of the square contributes to the moment of inertia. For each rod, the moment of inertia about its own center is m12, but we need to use the parallel axis theorem to find the moment of inertia about the center of the square.
The distance from the center of the square to the center of each rod (which is at a distance of 12 meter) is:
d=12
Thus, the moment of inertia for each rod about the center of the square is:
I=m12+m(12)2=m12+m4=m12+3m12=4m12=m3
5. Total Moment of Inertia for the Square:
Since there are four rods, the total moment of inertia Itotal for the square structure is:
Itotal=4×m3=4m3
6. Relate to Given Moment of Inertia I:
From the earlier calculation, we know that I=m12. Therefore, we can express m in terms of I:
m=12I
Substituting this back into the total moment of inertia:
Itotal=4(12I)3=16I
Final Answer:
The moment of inertia of the square structure about the perpendicular axis through its center is:
16I
The moment of inertia I of a thin rod of length L about an axis perpendicular to its length and through its center is given by the formula:
I=mL212
Here, L=1 meter, so we can denote the moment of inertia of one rod as:
I=m(12)12=m12
When we arrange four such rods to form a square, each rod will be positioned at the sides of the square. The length of each side of the square is 1 meter.
To find the moment of inertia of the square structure about an axis perpendicular to the plane of the square and through its center, we can use the perpendicular axis theorem. According to this theorem:
Iz=Ix+Iy
where Iz is the moment of inertia about the perpendicular axis, and Ix and Iy are the moments of inertia about the two axes in the plane of the square.
Each side of the square contributes to the moment of inertia. For each rod, the moment of inertia about its own center is m12, but we need to use the parallel axis theorem to find the moment of inertia about the center of the square.
The distance from the center of the square to the center of each rod (which is at a distance of 12 meter) is:
d=12
Thus, the moment of inertia for each rod about the center of the square is:
I=m12+m(12)2=m12+m4=m12+3m12=4m12=m3
Since there are four rods, the total moment of inertia Itotal for the square structure is:
Itotal=4×m3=4m3
From the earlier calculation, we know that I=m12. Therefore, we can express m in terms of I:
m=12I
Substituting this back into the total moment of inertia:
Itotal=4(12I)3=16I
The moment of inertia of the square structure about the perpendicular axis through its center is:
16I
Similar Questions
Figure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View Solutionradius R are joined to the ends of a weightless rod of length 2R. The M.I. of the system about the perpendicular axis through its centre will be
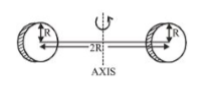
View Solution
Knowledge Check
The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
AI4BI2C2ID4IThe M.I. of a thin rod about a normal axis through its centre is I. It is bent at the centre suh that the two parts are perpendicular to each other and perpendicular to the axis. The M.I. Of the sytem about the same axis will be
A2IBICI/2D4IThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
AI4BI2C2ID4I
If I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
View SolutionM.I. of a thin uniform circular disc about one of the diameters is I. Its M.I. about an axis perpendicular to the plane of disc and passing through its centre is
View SolutionI is moment of inertia of a thin square plate about an axis passing through opposite corners of plate. The moment of inertia of same plate about an axis perpendicular to the plane of plate and passing through its centre is
View SolutionThe moment of inertia of uniform circular disc about an axis passing through its centre is 6kgm2 . Its M.I. about an axis perpendicular to its plane and just touching the rim will be
View SolutionThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
View Solution
