A concave mirror of radius of curvature 60 cm is placed at the bottom of tank containing water upto a height of 20 cm. The mirror faces upwards with its axis vertical. Solar light falls normally on the surface of water and the image of the sun is formed. If aμw=43 then with the observer in air, the distance of the image from the surface of water is:
30 cm
10 cm
7.5 cm above
7.5 cm below
The correct Answer is:C
To solve the problem step by step, we will follow the principles of optics and the properties of concave mirrors.
Step 1: Determine the Focal Length of the Concave Mirror
The radius of curvature (R) of the concave mirror is given as 60 cm. The focal length (f) of a concave mirror is given by the formula:
f=R2
Substituting the value of R:
f=60cm2=30cm
Step 2: Identify the Position of the Image in Water
Since solar rays fall normally on the surface of the water, they will reflect off the mirror. The image formed by the concave mirror will be at the focal point, which is 30 cm above the mirror. However, we need to consider the height of the water.
The mirror is at the bottom of the tank, and the water level is 20 cm above the mirror. Therefore, the position of the image relative to the water surface is:
Distance of image from water surface=Height of water−Focal length
=20cm−30cm=−10cm
This indicates that the image is actually formed 10 cm below the water surface.
Step 3: Calculate the Apparent Shift Due to Refraction
Since the observer is in air and the image is formed in water, we need to account for the apparent shift due to the refractive index (μ) of water. The refractive index of water is given as μ=43.
The relation between real distance (d_real) and apparent distance (d_apparent) is given by:
drealdapparent=μ
Rearranging this gives:
dapparent=drealμ
Here, dreal=10cm (the distance below the water surface), so:
dapparent=10cm43=10×34=7.5cm
Step 4: Determine the Final Position of the Image from the Water Surface
Since the apparent distance is 7.5 cm below the water surface, the distance of the image from the water surface is:
Distance of image from water surface=20cm−7.5cm=12.5cm
Final Answer
Thus, the distance of the image from the surface of the water is:
Distance of the image from the surface of water=12.5cm
The radius of curvature (R) of the concave mirror is given as 60 cm. The focal length (f) of a concave mirror is given by the formula:
f=R2
Substituting the value of R:
f=60cm2=30cm
Since solar rays fall normally on the surface of the water, they will reflect off the mirror. The image formed by the concave mirror will be at the focal point, which is 30 cm above the mirror. However, we need to consider the height of the water.
Distance of image from water surface=Height of water−Focal length
=20cm−30cm=−10cm
This indicates that the image is actually formed 10 cm below the water surface.
Since the observer is in air and the image is formed in water, we need to account for the apparent shift due to the refractive index (μ) of water. The refractive index of water is given as μ=43.
drealdapparent=μ
Rearranging this gives:
dapparent=drealμ
dapparent=10cm43=10×34=7.5cm
Since the apparent distance is 7.5 cm below the water surface, the distance of the image from the water surface is:
Distance of image from water surface=20cm−7.5cm=12.5cm
Thus, the distance of the image from the surface of the water is:
Distance of the image from the surface of water=12.5cm
Similar Questions
A concave mirror of radius of curvature one meter is placed at the bottom of a tank of water. The mirror forms an image of the sun when it is directly overhead. Calculate the distance of the images from the mirror for (a) 80cm and (b) 40cm of water in the tank ( μ=4/3 for water)
View SolutionA concave mirror of focal length 20cm is placed inside water with its shining surface upwards and principal axis vertical as shown in Fig. Rays are incident parallel to the principal, axis of concave mirror. Find the position of final image.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
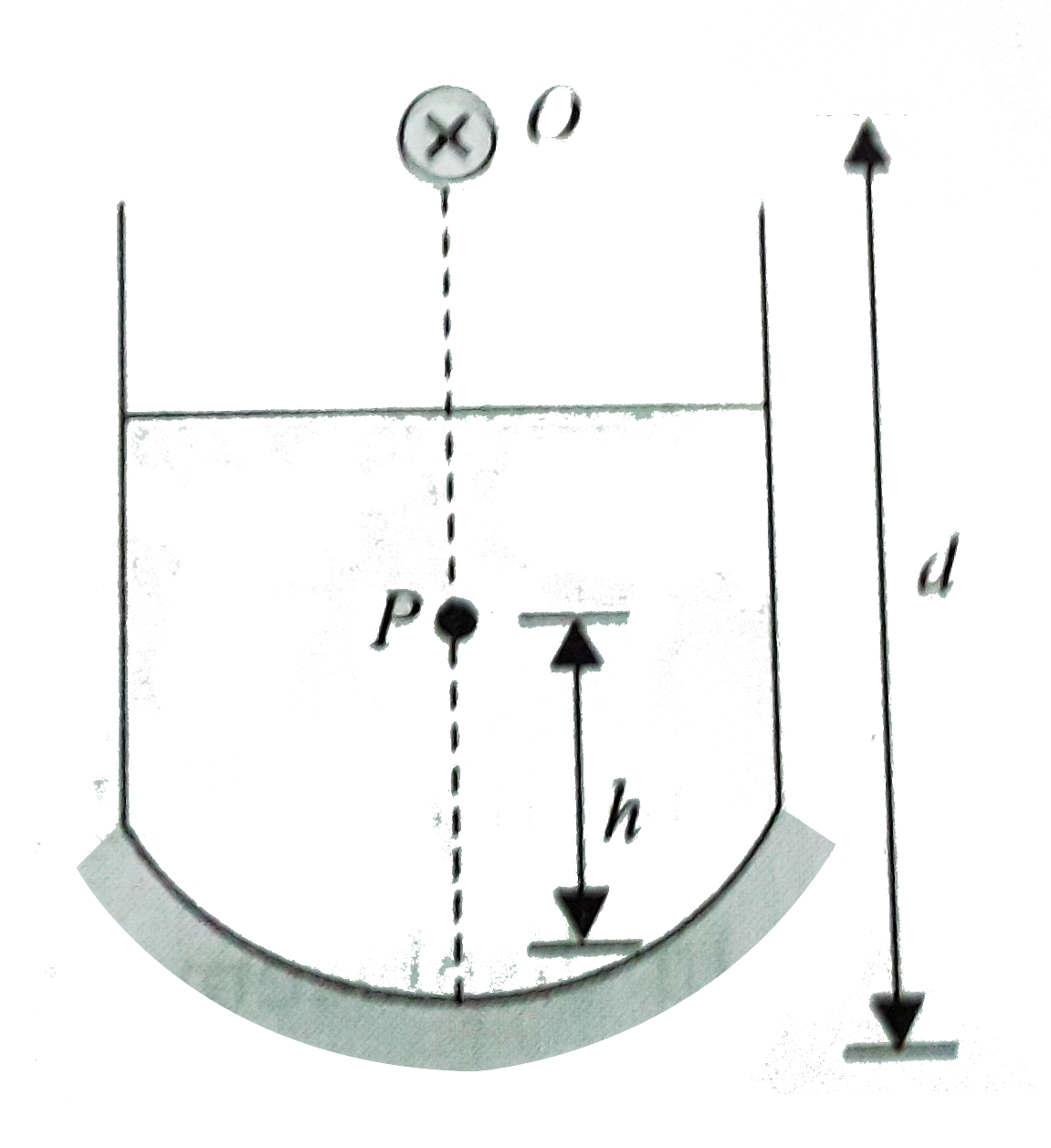 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμ - Question 2 - Select One
A concave mirror is placed at the bottom of an empty tank with face upwards and axis vertical. When sunlight falls normally on the mirror, it is focussed at distance of 32cm from the mirror. If the tank filled with water (μ=4/3) up to a height of 20cm, then the sunlight will now get focussed at
A16cm above water levelB9cm above water levelC24cm below water levelD9cm below water level - Question 3 - Select One
A concave mirror of radius of curvature 20 cm forms image of the sun. The diameter of the sun subtends an angle 1∘ on the earth. Then the diameter of the image is (in cm) :
A2π/9Bπ/9C20Dπ/18
A concave mirror of focal length 10 cm is placed at a distance of 35 cm from a wall. How far from the wall an object be placed so that its image formed by the mirror falls on the wall?
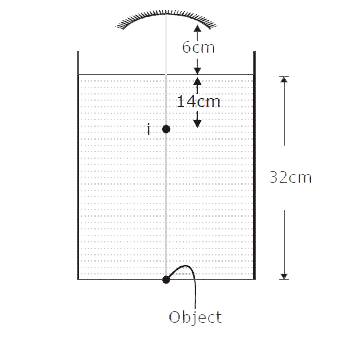
View SolutionA beaker contains water (μ=4/3) filled to a height of 32 cm. A concave mirror is fixed 6 cm above the surface of water as shown in figure. An object is placed at the bottom of the beaker and its image is formed 14 cm below the surface of water. The focal length of the mirror is
 View Solution
View SolutionImage formed by a concave mirror radius of curvature 40 cm is half the size of the object. Then distance of object and its image from the mirror will be -
View SolutionA concave mirror of radius of curvature 40cm forms an image of an object placed on the principal axis at a distance 45 cm in front of it. Now if the system (including object) is completely immersed in water (μ=1.33) , then
View SolutionWater is filled in a container upto a height of 5cm. There is a concave mirror of radius of curvature 40cm. A person just above the surface observes image of 'A'. The distance of image from water surface is (μwater=1.33):
_2019_CBT7_E01_003_Q01.png) View Solution
View Solution

