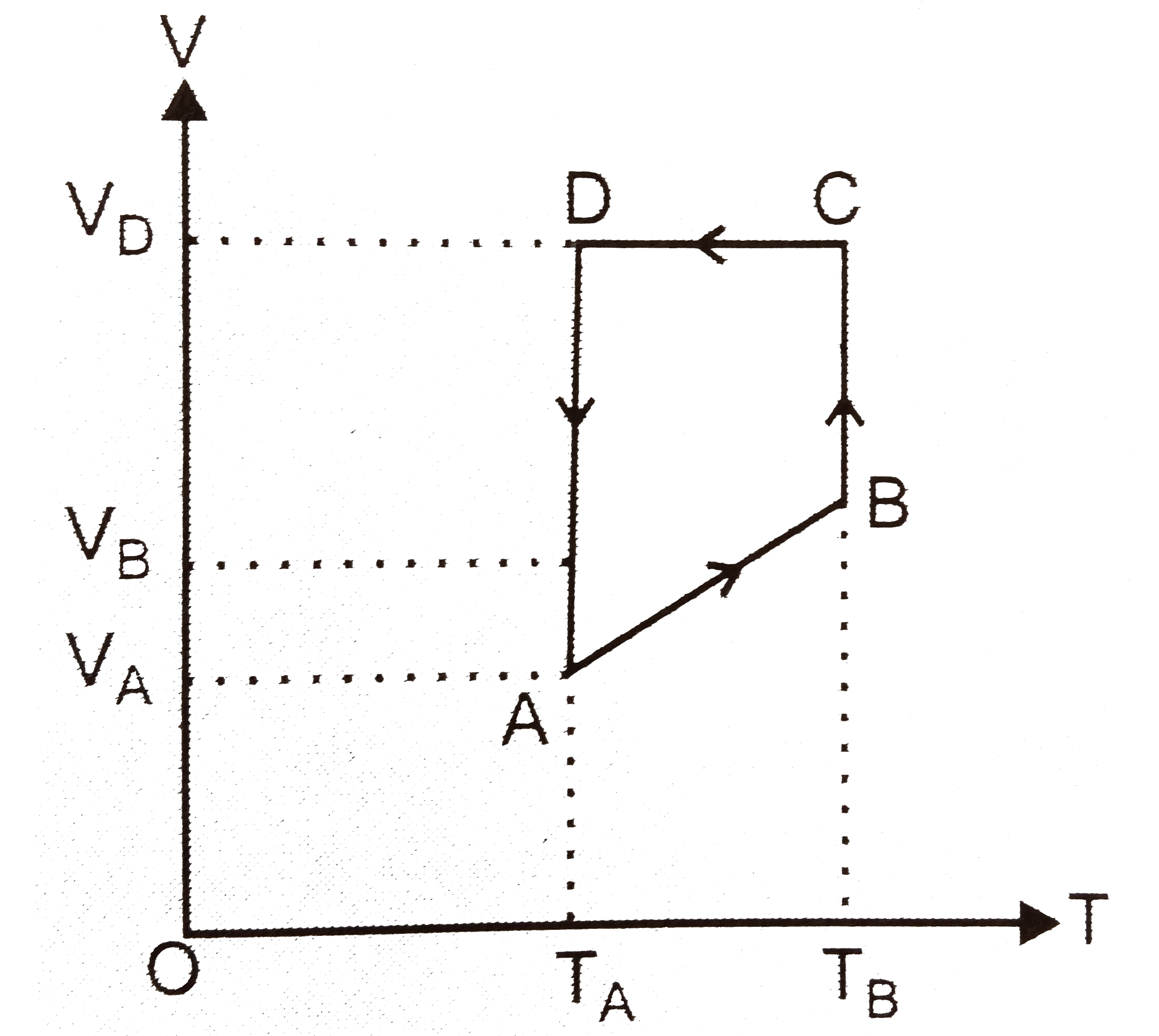
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.

The respective cyclic process is shown in Figure-3.52. The expansion and compression ratio are given as
VAVB=16 and VCVB=2
In adiabatic process AB, we have
TAVγ−1A=TBVγ−1B
or TB=TA(VAVB)γ−1
=300×(16)0.4
=909 K
Similarly for isobaric process BC, we have
TCVC=TBVB
or TC=TB(VCVB) ....(3.119)
= 909 x 2 = 1818 K
Similarly for adiabatic process CD we have
TCVγ−1C=TDVγ−1D
or TD=TC(VCVD)γ−1
As we have VD=VA, thus
VCVD=VCVA=VCVB×VBVA
=2×116=18
Thus from equation-(3.119)
TD=1818×(18)0.4
=791.3 K
The efficiency of cycle can be given as
η=1−∣∣∣QoutQin∣∣∣
Here we know in process AB and CD, as being adiabatic processes no heat exchange takes place and in isobaric process BC as temperature ofgas increases, heat is taken in (say Q1 ) and it is given as
Q1=nCP(TC−TB)...(3.120)
Similarly in isochoric process DA as temperature of gas decreases heat is rejected (say Q2) and it can be given as
Q2=nCP(TD−TA) [ A magnitude of rejected heat]
Now efficiency of this cycle can be given as
η=1−∣∣∣QoutQin∣∣∣
=1−Q2Q1
=1−CV(TD−TA)CP(TC−TB)
=TD−TAγ(TC−TB)
=(791.3−300)(1.4)(1818−909)
=1−491.31272.6=0.614=61.4%
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Discussion Question17videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct21videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems42videos
PHOTOELECTRIC EFFECT AND MATTER WAVES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems28videos
WAVE OPTICS
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown figure. The volume rations are VBVA=2andVDVA=4 If the temperature fTAatAis27∘C.
 Calculate,View Solution
Calculate,View Solution
Knowledge Check
- Question 1 - Select One
An ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state
 AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the process
AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the process - Question 2 - Select One
One mole of an ideal gas is taken through a cyclic process as shown in the V-T diagram. Which of the following statements is true ?
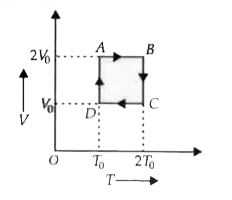 AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2.
AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2. - Question 3 - Select One
A monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
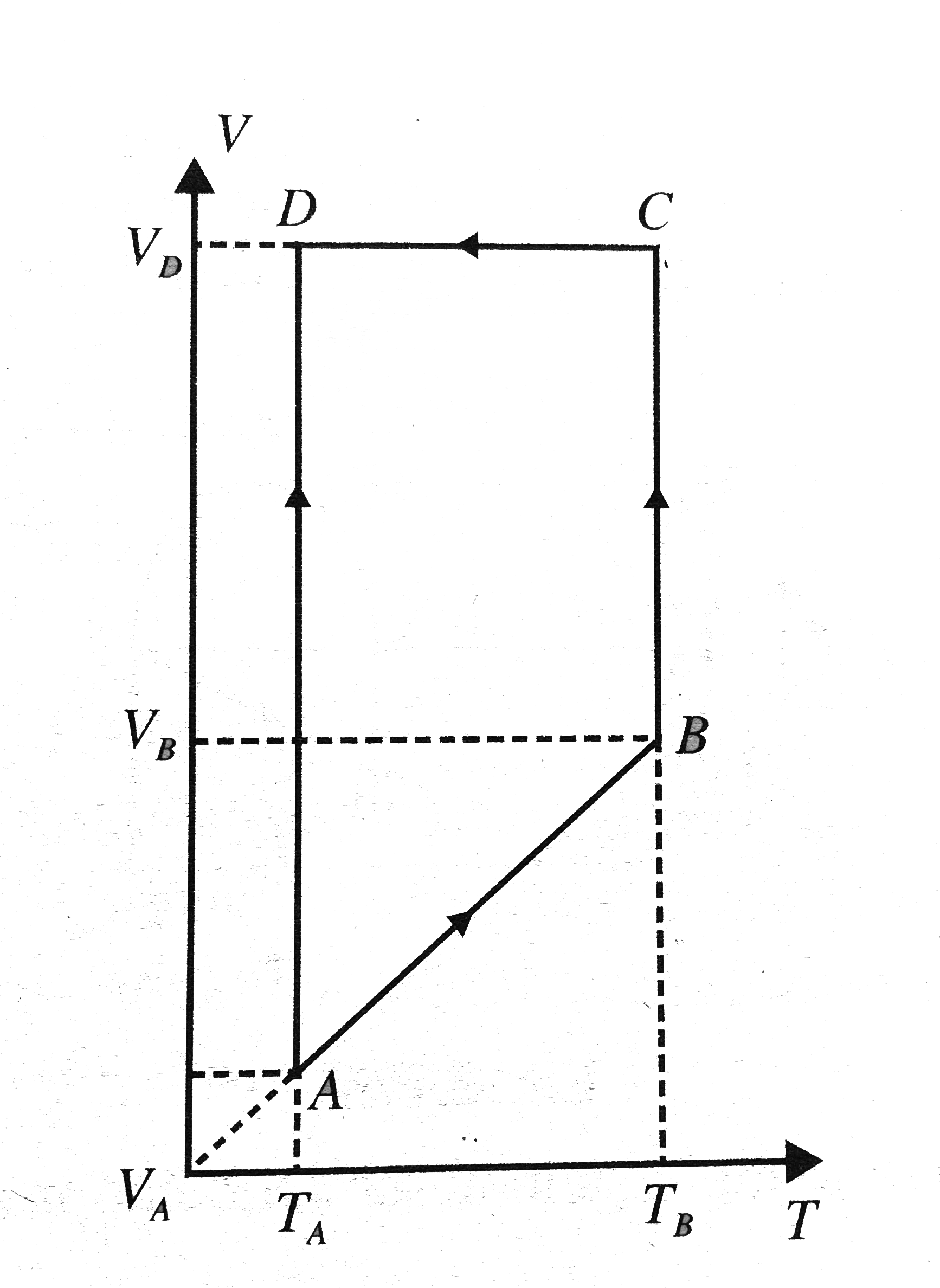
The temperature of the gas at point BA500KB700KC600KD300K
A mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate
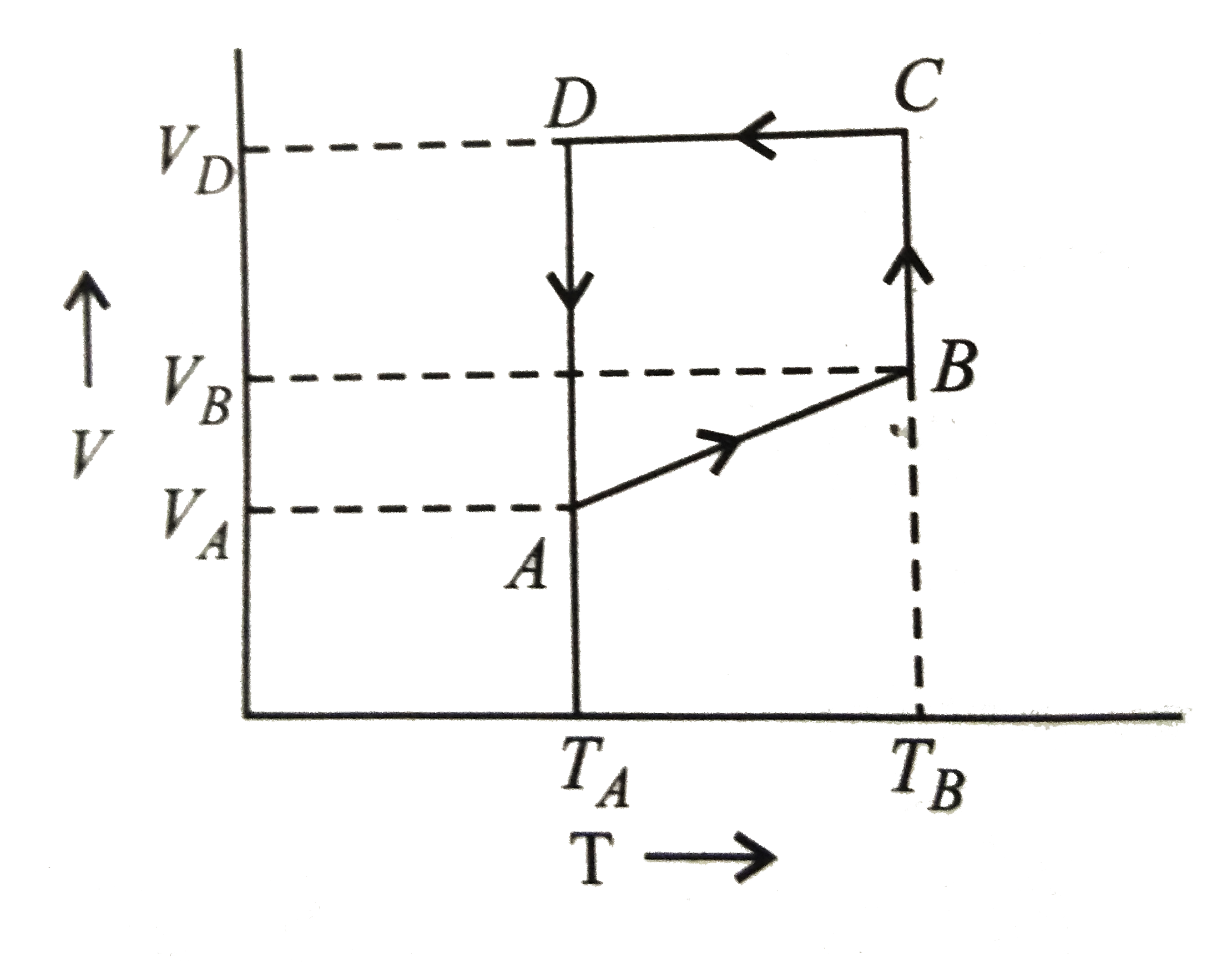
a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total wrok done in cyclic process.View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2andVDVA=4. If the temperature TA at A is 27∘C.
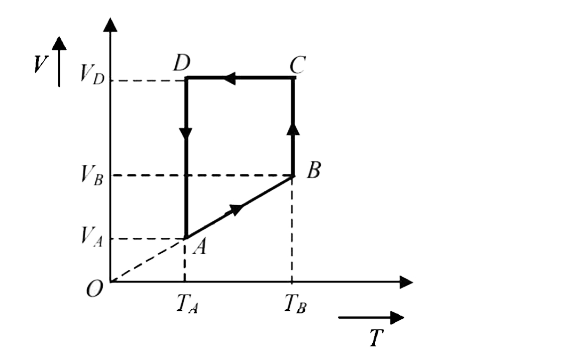
Calculate,
(a) the temperature of the gas at point B,
(b) heat absorbed or released by the gas in each process,
(c) the total work done by the gas during the complete cycle. Express your answer in terms of the gas constant R.View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2 and VDVA=4. If the temperature TA at A is 27∘C, calculate:
(a) The temperature of the gas at point B.
(b) Heat absorbed or released by the gas in each process.
(c) The total work done by the gas during complete cycle.View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
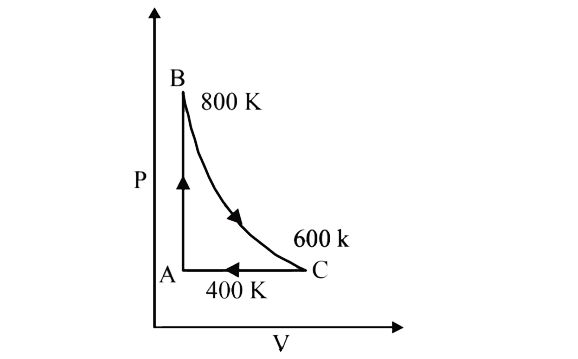 View Solution
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
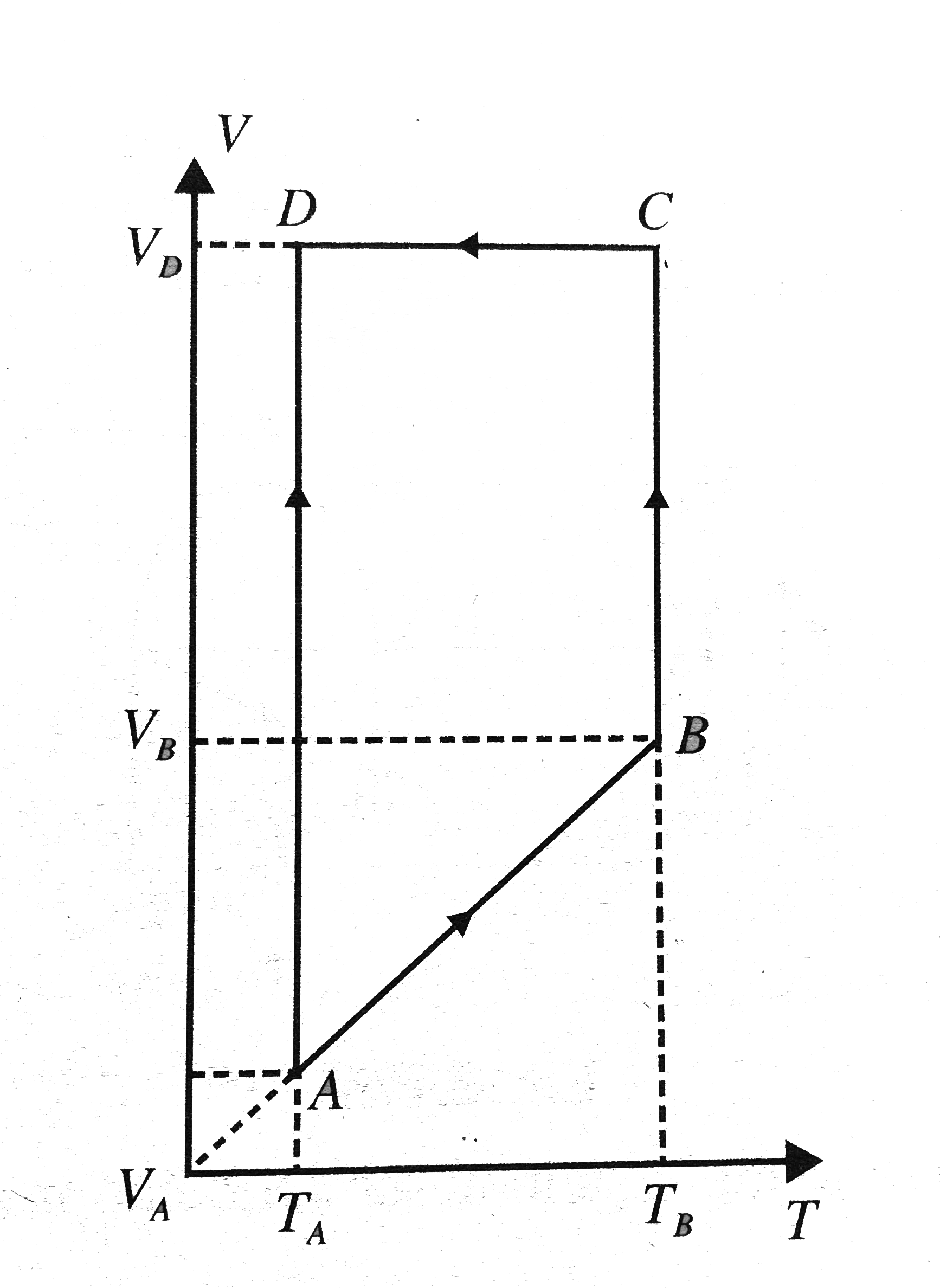
The total work done by the gas during the complete cycle.View Solution

