One mole of an ideal gas at temperature T was cooled isochorically till the gas pressure fell from P to Pn. Then, by an isobaric process, the gas was restored to the initial temperature. The net amount of heat absorbed by the gas in the process is
nRT
RTn
RT(1−n−1)
RT(n−1)
Step by step video & image solution for One mole of an ideal gas at temperature T was cooled isochorically till the gas pressure fell from P to (P)/(n). Then, by an isobaric process, the gas was restored to the initial temperature. The net amount of heat absorbed by the gas in the process is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Advance MCQs with One or More Options Correct10videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Unsolved Numerical Problems100videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct21videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems42videos
PHOTOELECTRIC EFFECT AND MATTER WAVES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems28videos
WAVE OPTICS
Similar Questions
Two moles of an ideal gas at temperature T0=300K was cooled isochorically so that the pressure was reduced to half. Then, in an isobaric process, the gas expanded till its temperature got back to the initial value. Find the total amount of heat absorbed by the gas in the processs
View SolutionTwo moles of a certain ideal gas at temperature T0= 300 K were cooled isochorically so that the gas pressure reduced η= 2.0 times. Then, as a result of the isobaric process, the gas expanded till its temperature get back to the initial value. Find the total amount of heat absorbed by the gas in this process.
View Solution
Knowledge Check
- Question 1 - Select One
n' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
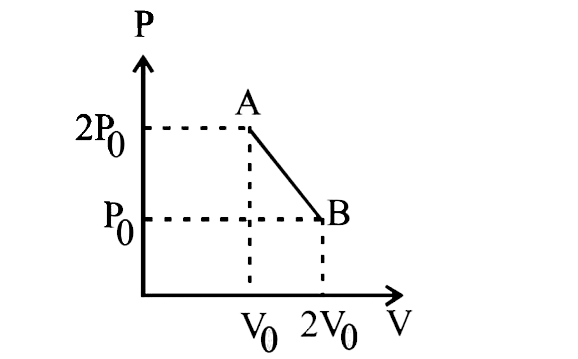 A9P0V02nRB9P0V0nRC9P0V04nRD3P0V02nR
A9P0V02nRB9P0V0nRC9P0V04nRD3P0V02nR - Question 2 - Select One
One mole of an ideal gas at temperature T1 expends according to the law PV2=a (constant). The work done by the gas till tempereature of gas becomes T2 is
A12R(T2−T1)B13R(T2−T1)C14R(T2−T1)D15R(T2−T1) - Question 3 - Select One
In a process V∝T2, temperature of 2 moles of a gas is increased by 200K. Work done by the gas in this process will be
A600 RB800 RC1000 RD1200 R
Two moles of a certain gas at a temperature T0=300K were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.
View SolutionTwo moles of a certain ideal gas at 300K were cooled at constant volume so that the pressure was reduced to half t he initial value. Then, as a result of heating at constant pressure, the gas expanded till its temperature got back ot the initial value. Find the total amount of heat absorbed by the gas in the process.
View SolutionTwo moles of a certain ideal gas at 300K is cooled at constant volume so that the pressure is reduced to half the original value. Now the gas is heated at constant pressure so that its temperature becomes equal to the initial temperature. Find the total amount of heat absorbed by the gas in the process.
View SolutionOne mole of monoatomic gas is taken round the cyclic process. Heat absorbed by gas in process AB is
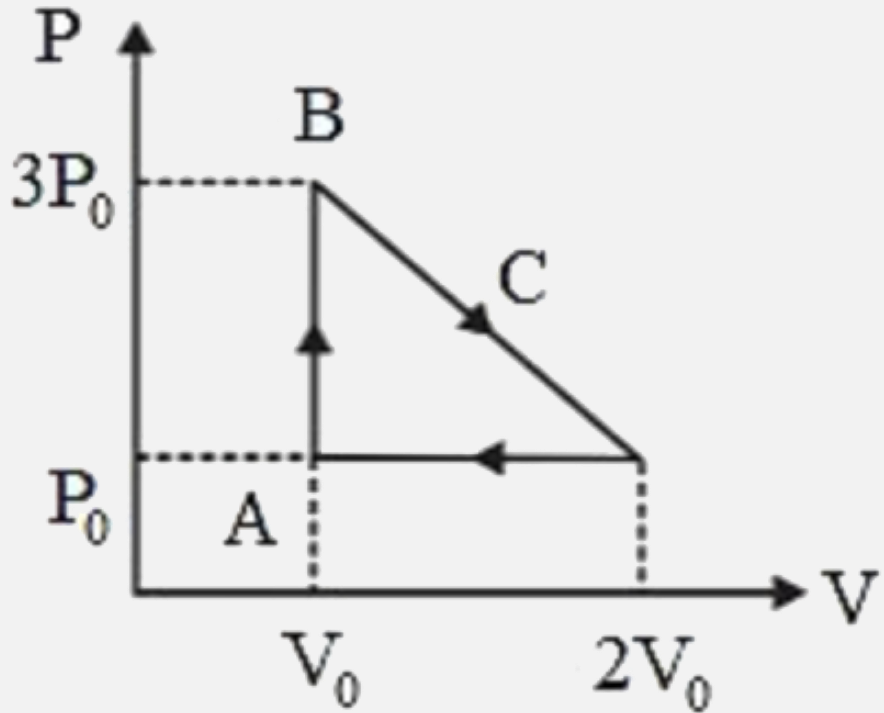 View Solution
View SolutionTwo moles of an ideal gas are cooled isochorically and then expanded isobarically to lower the gas temperature back to the initial value. Find the entropy increment of the gas if in this process the gas pressure changed n=3.3 times.
View Solution

