A horizontal insulated cylinder is provided with frictionless non-conducting piston. On each side of the piston there is 50 litres of air at a pressure of 1 atmosphere and 273 K. Heat is slowly supplied to the air at the left hand side, until the piston has compressed the air on the right hand side to 2.5 atmosphere. Find Work done on the air on the right hand side
The correct Answer is:−3741.5J
To solve the problem of finding the work done on the air on the right-hand side of the piston, we will follow these steps:
Step 1: Understand the Initial Conditions
We start with 50 liters of air at a pressure of 1 atmosphere and a temperature of 273 K on both sides of the piston.
Step 2: Convert Units
Convert the volume from liters to cubic meters for standard SI units:
V=50 liters=50×10−3 m3=0.05 m3
Step 3: Determine the Final Conditions
The problem states that the pressure on the right side of the piston is compressed to 2.5 atmospheres. We need to convert this pressure to pascals:
Pfinal=2.5 atm=2.5×101325 Pa=253312.5 Pa
Step 4: Calculate the Work Done
The work done on the gas can be calculated using the formula for work done on a gas during an isothermal process:
W=PΔV
However, since the volume on the right side is compressed, we need to find the change in volume. Initially, the volume on the right side is 0.05 m³, and we need to find the final volume when the pressure is 2.5 atm.
Using the ideal gas law, we can find the final volume:
PV=nRT
Assuming the number of moles (n) and the temperature (T) remain constant, we can set up the equation:
P1V1=P2V2
Where:
- P1=1 atm=101325 Pa
- V1=0.05 m3
- P2=2.5 atm=253312.5 Pa
Rearranging gives:
V2=P1V1P2=101325×0.05253312.5≈0.020 m3
Step 5: Calculate the Change in Volume
The change in volume (ΔV) is:
ΔV=Vfinal−Vinitial=0.020−0.05=−0.030 m3
Step 6: Calculate Work Done
Now, substituting the values into the work done formula:
W=PfinalΔV=253312.5×(−0.030)≈−7599.375 J
The work done on the gas is approximately 7599.375 J (the negative sign indicates work is done on the gas).
Final Answer
The work done on the air on the right-hand side is approximately 7599.375 J.
---
We start with 50 liters of air at a pressure of 1 atmosphere and a temperature of 273 K on both sides of the piston.
Convert the volume from liters to cubic meters for standard SI units:
V=50 liters=50×10−3 m3=0.05 m3
The problem states that the pressure on the right side of the piston is compressed to 2.5 atmospheres. We need to convert this pressure to pascals:
Pfinal=2.5 atm=2.5×101325 Pa=253312.5 Pa
The work done on the gas can be calculated using the formula for work done on a gas during an isothermal process:
W=PΔV
However, since the volume on the right side is compressed, we need to find the change in volume. Initially, the volume on the right side is 0.05 m³, and we need to find the final volume when the pressure is 2.5 atm.
PV=nRT
Assuming the number of moles (n) and the temperature (T) remain constant, we can set up the equation:
P1V1=P2V2
Where:
- P1=1 atm=101325 Pa
- V1=0.05 m3
- P2=2.5 atm=253312.5 Pa
V2=P1V1P2=101325×0.05253312.5≈0.020 m3
The change in volume (ΔV) is:
ΔV=Vfinal−Vinitial=0.020−0.05=−0.030 m3
Now, substituting the values into the work done formula:
W=PfinalΔV=253312.5×(−0.030)≈−7599.375 J
The work done on the gas is approximately 7599.375 J (the negative sign indicates work is done on the gas).
The work done on the air on the right-hand side is approximately 7599.375 J.
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.1
6 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.3
10 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Advance MCQs with One or More Options Correct
10 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
A horizontal insulated cylinder is provided with frictionless non-conducting piston. On each side of the piston there is 50 litres of air at a pressure of 1 atmosphere and 273 K. Heat is slowly supplied to the air at the left hand side, until the piston has compressed the air on the right hand side to 2.5 atmosphere. Find Heat added to air on the left hand side.
View SolutionA horizontal insulated cylinder is provided with frictionless non-conducting piston. On each side of the piston there is 50 litres of air at a pressure of 1 atmosphere and 273 K. Heat is slowly supplied to the air at the left hand side, until the piston has compressed the air on the right hand side to 2.5 atmosphere. Find : Final temperature of air on the right hand side
View Solution
Knowledge Check
A cylinder fitted with a piston contains 0.2 moles of air at temperature 27∘ . The piston is pushed so slowly that the air within the cylinder remains in thermal equilibrium with the surroundings. Find the approximate work done by the system if the final volume is twice the initial volume
A543 jB345 jC453 jD600j
A horizontal insulated cylinder is provided with frictionless non-conducting piston. On each side of the piston there is 50 litres of air at a pressure of 1 atmosphere and 273 K. Heat is slowly supplied to the air at the left hand side, until the piston has compressed the air on the right hand side to 2.5 atmosphere. Find Final temperature of air on the left hand side
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
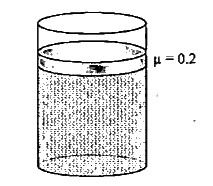
View SolutionFigure-2.47 shows a cylindrical container of radius 5cm and a piston is fitted in it to enclose a length of 20 cm in it.The cylinder contains an ideal gas at a pressure of 1 atmosphere and 300 K temperature.The cylinder is slowly heated and it is found that the piston starts displacing when the gas temperature reaches 600 K. It is given that the friction coefficient between the piston sidesand the container wall is 0.2. Find the normal force acting between piston sides and the container wall per unit length ofits circumference.
View SolutionOne gram of saturated vapour is enclosed in a thermally insulated cylinder under a weightless piston. The outside pressure is standard m=1g of water is introduced into the cylinder at a temperature t0=22∘C. Neglecting the heat capacity of the cylinder and piston and friction, find the work done by the force of the atmosphere during the lowering of the piston. T= temperature of saturated vapour =373K,L sp. heat latent heat =12250/kJ/kg
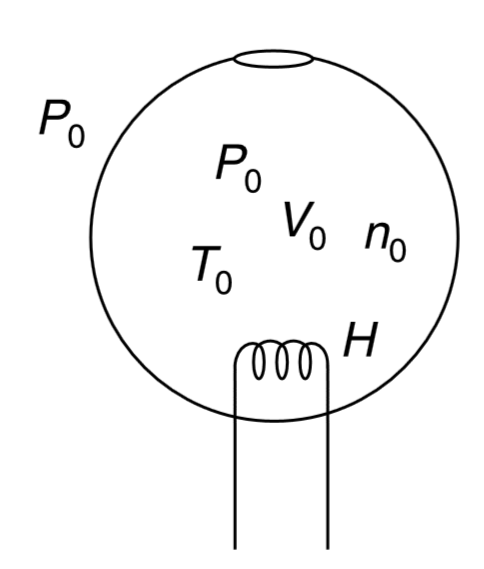
View SolutionA spherical container made of non conducting wall has a small orifice in it. Initially air is filled in it at atmospheric pressure (P0) and atmospheric temperature (T0). Using a small heater, heat is slowly supplied to the air inside the container at a constant rate of H J/s. Assuming air to be an ideal diatomic gas find its temperature as a function of time inside the container.
View SolutionA cylinder contains 3 moles of oxygen at a temperature of 27∘C. The cylinder is provided with a frictionless piston which maintains a constant pressure of 1 atm on the gas. The gas is heated until its temperature rises to 127∘C.
a. How much work is done by the gas in the process ?
b. What is the change in the internal energy of the gas ?
c. How much heat was supplied to the gas ?
For oxygen CP=7.03calmol−1.∘C−1.
View SolutionA cylinder is fitted with a piston, beneath which is a spring, as in the figure. The cylinder is open at the top. Friction is absent. The spring is 3600N/m. The piston has a negligible mass and a radius of 0.025m (a) when air beneath the piston is conpletely pumped out, how much does the atmospheric pressure cause the spring to compress? (b) How much work does the atmospheric pressure do in compressing the spring?

View Solution
