A cylinder with a movable piston is filled at 25∘C with a gas that occupies a volume of 30.5cm3. If the maximum capacity of the cylinder is 45.8cm3, what is the highest temperature to which the cylinder can be heated at constant pressure without having the piston come out?
50∘C
147.5∘C
174.5∘C
120∘C
The correct Answer is:C
To solve the problem, we will use Charles's Law, which states that for a given mass of gas at constant pressure, the volume of the gas is directly proportional to its absolute temperature (in Kelvin). The formula can be expressed as:
V1T1=V2T2
Where:
- V1 = initial volume of the gas
- T1 = initial temperature of the gas in Kelvin
- V2 = final volume of the gas (maximum capacity of the cylinder)
- T2 = final temperature of the gas in Kelvin (which we want to find)
Step 1: Convert the initial temperature to Kelvin
The initial temperature T1 is given as 25∘C. To convert this to Kelvin, we use the formula:
T(K)=T(°C)+273.15
So,
T1=25+273.15=298.15K≈298K
Step 2: Identify the volumes
The initial volume V1 is given as 30.5cm3 and the maximum volume V2 is 45.8cm3.
Step 3: Set up the equation using Charles's Law
Using Charles's Law, we can set up the equation:
30.5298=45.8T2
Step 4: Solve for T2
Cross-multiplying gives us:
30.5⋅T2=45.8⋅298
Now, we can solve for T2:
T2=45.8⋅29830.5
Calculating the right side:
T2=13653.430.5≈447.4K
Step 5: Convert T2 back to Celsius
To convert T2 back to Celsius, we use the formula:
T(°C)=T(K)−273.15
So,
T2(°C)=447.4−273.15≈174.25°C≈174.4°C
Final Answer
The highest temperature to which the cylinder can be heated at constant pressure without having the piston come out is approximately 174.4 °C.
---
- V1 = initial volume of the gas
- T1 = initial temperature of the gas in Kelvin
- V2 = final volume of the gas (maximum capacity of the cylinder)
- T2 = final temperature of the gas in Kelvin (which we want to find)
The initial temperature T1 is given as 25∘C. To convert this to Kelvin, we use the formula:
The initial volume V1 is given as 30.5cm3 and the maximum volume V2 is 45.8cm3.
Using Charles's Law, we can set up the equation:
Cross-multiplying gives us:
To convert T2 back to Celsius, we use the formula:
The highest temperature to which the cylinder can be heated at constant pressure without having the piston come out is approximately 174.4 °C.
Similar Questions
A gas is enclosed in a cylinder with a freely movable piston. The load on the piston is gradually decreased. The temperature of the gas can be changed by placing the cylinder in hot and cold heat reservoirs. The figure shown P−Vgraph of such a cylinder. What intermediate can be drawn the nature of change in the temperature of the gas ?
 " "
" "  View Solution
View SolutionA cylinder and a cone have the same height and the same radius. The volume of the cylinder is 24cm3. What will be the volume of the cone?
View Solution
Knowledge Check
- Question 1 - Select One
If the volume and curved surface area of a cylinder are 269.5cm3 and 154cm2 respectively , what is the height of the cylinder ?
A6B3.5C7Dcan't be determined - Question 2 - Select One
If the volume and curved surface area of a cylinder are 269.5cm3 and 154cm2 respectively , what is the height of the cylinder ?
A6B3.5C7Dcan't be determined - Question 3 - Select One
Suppose a monatomic ideal gas is contained within a vertical cylinder that is fitted with a movable piston. The piston is frictionless and has a negligible mass. The area of the piston is3.14×10−2m2, and the pressure outside the cylinder is 1.01×105 Pa. Heat (2093 J) is removed from the gas. Through what distance does the piston drop?
A0.185mB0.389mC0.539mD0.264m
The piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
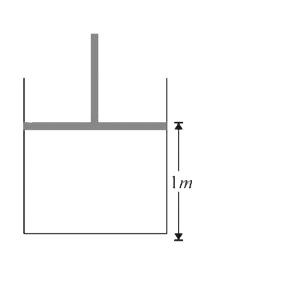
Find the new height (in m) of the piston above the base of the cylinder.View SolutionA gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory why on pulling the piston out, the pressure of decreases.
View SolutionA mass less piston divides a thermally insulated cylinder into two parts having volumes V = 2.5 litre and 3 V = 7.5 litre. 0.1 mole of an ideal gas is confined into the part with volume V at a pressure of P=105N/m2. The other part of the cylinder is empty. The piston is now released and the gas expands to occupy the entire volume of the cylinder. Now the piston is pressed back to its initial position. Find final temperature of the gas.
[Take R=253Jmol−1K−1 and γ=1.5 for the gas]View SolutionFigure-2.47 shows a cylindrical container of radius 5cm and a piston is fitted in it to enclose a length of 20 cm in it.The cylinder contains an ideal gas at a pressure of 1 atmosphere and 300 K temperature.The cylinder is slowly heated and it is found that the piston starts displacing when the gas temperature reaches 600 K. It is given that the friction coefficient between the piston sidesand the container wall is 0.2. Find the normal force acting between piston sides and the container wall per unit length ofits circumference.
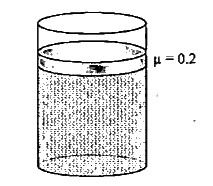 View Solution
View SolutionShow that the maximum volume of the cylinder which can be inscribed in a sphere of radius 5√3cm is 500πcm3.
View Solution

