A vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
ˆi+ˆj
4ˆi
ˆi+ˆk
−7ˆk
The correct Answer is:D
To solve the problem, we need to analyze the conditions given in the question.
1. Understanding the Given Information:
- We have a vector →A that is along the positive z-axis. This can be represented as:
→A=A^k
where A is the magnitude of the vector and ^k is the unit vector in the z-direction.
2. Vector Product Condition:
- We are told that the vector product (cross product) of →A and another vector →B is zero:
→A×→B=0
- The cross product of two vectors is zero if the vectors are parallel or if one of the vectors is the zero vector.
3. Determining the Direction of →B:
- Since →A is along the z-axis, for →A×→B=0, vector →B must also be parallel to →A. This means →B can be expressed as:
→B=B^k
where B is some scalar multiple.
4. Analyzing the Given Options:
- We need to check which of the given options can be expressed as a multiple of ^k:
1. ^i+^j (not parallel to ^k)
2. 4^i (not parallel to ^k)
3. ^i+^k (not purely along ^k)
4. −7^k (this is parallel to ^k)
5. Conclusion:
- The only vector from the options that is parallel to →A (which is along the z-axis) is:
→B=−7^k
- Therefore, the answer is:
→B=−7^k
Final Answer:
→B=−7^k
- We have a vector →A that is along the positive z-axis. This can be represented as:
→A=A^k
where A is the magnitude of the vector and ^k is the unit vector in the z-direction.
- We are told that the vector product (cross product) of →A and another vector →B is zero:
→A×→B=0
- The cross product of two vectors is zero if the vectors are parallel or if one of the vectors is the zero vector.
- Since →A is along the z-axis, for →A×→B=0, vector →B must also be parallel to →A. This means →B can be expressed as:
→B=B^k
where B is some scalar multiple.
- We need to check which of the given options can be expressed as a multiple of ^k:
1. ^i+^j (not parallel to ^k)
2. 4^i (not parallel to ^k)
3. ^i+^k (not purely along ^k)
4. −7^k (this is parallel to ^k)
- The only vector from the options that is parallel to →A (which is along the z-axis) is:
→B=−7^k
- Therefore, the answer is:
→B=−7^k
→B=−7^k
Similar Questions
Knowledge Check
- Question 1 - Select One
A vector →A is along the positive x-axis and its vector product with another vector →B is zero, then vector →B could be
Aˆi+ˆjB4ˆiCˆj+ˆkD−7ˆk - Question 2 - Select One
A vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
A4jB−4iC−(i+j)D(j+k) - Question 3 - Select One
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .A120B90C60D150
.A120B90C60D150
The magnitude of the vector product of two vectors →A and →B may not be:
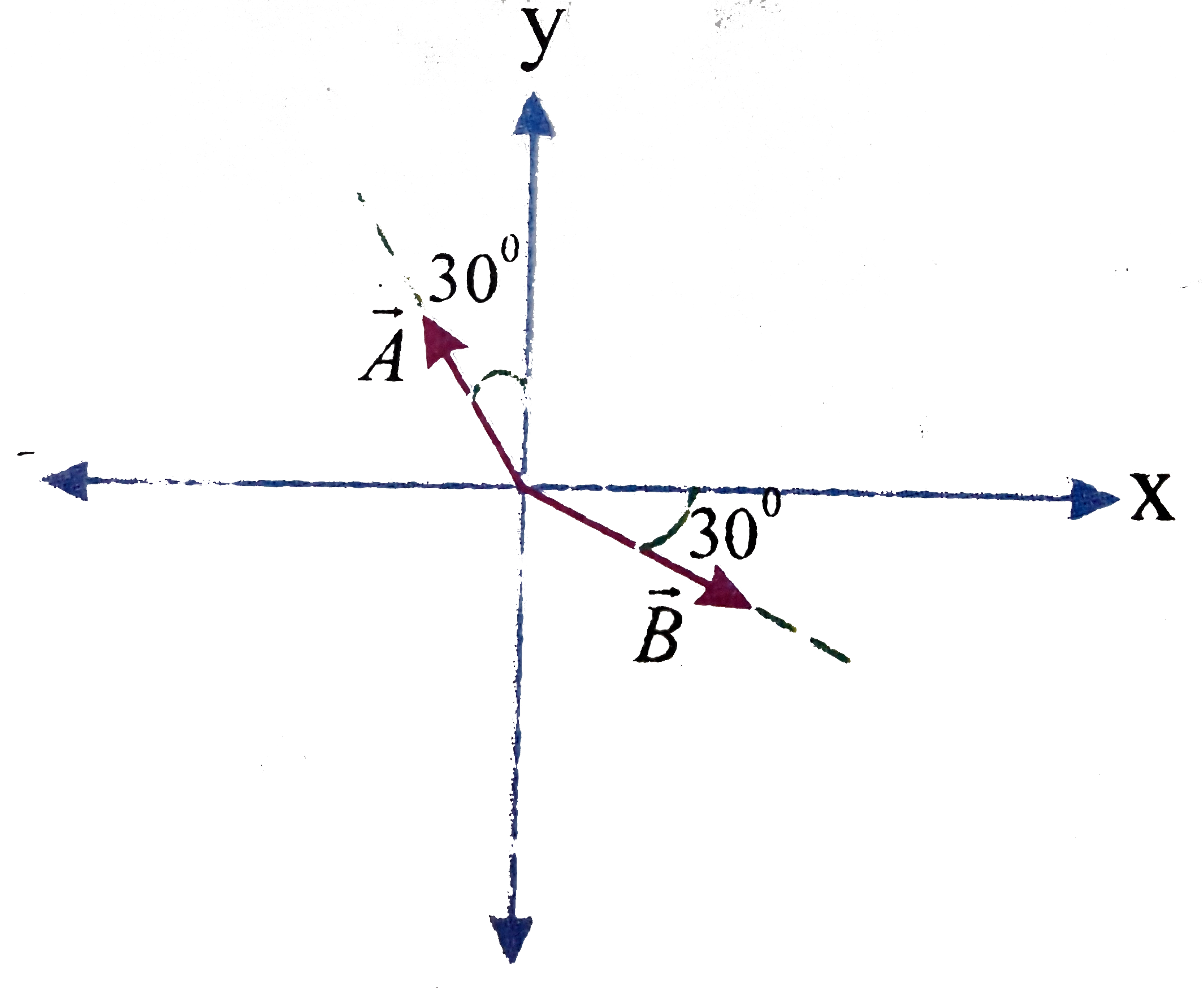
View SolutionA vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
 View Solution
View SolutionThe magnitude of the vectors product of two vectors ∣∣→A∣∣and∣∣→B∣∣ may be
View SolutionVector →A−→B represents -
View SolutionResolved part of vector →a and along vector →b is →a1 and that prependicular to →b is →a2 then →a1×→a2 is equl to
View Solution

