Centripetal force (F) on a body of mass (m) moving with uniform speed (v) in a circle of radius (r ) depends upon m, v and r. The formula for the centripetal force using theory of dimensons.
kmv2
kmv2r
km2v2r
km2vr
The correct Answer is:B
To derive the formula for centripetal force (F) using dimensional analysis, we will follow these steps:
Step 1: Identify the Variables
The centripetal force depends on three variables:
- Mass (m)
- Velocity (v)
- Radius (r)
Step 2: Write the Dimensional Formulae
Next, we need to write the dimensional formulae for each of these variables:
- Mass (m) has the dimensional formula: (M)
- Velocity (v) is distance per time, so its dimensional formula is: (L)(T)−1
- Radius (r) is a length, so its dimensional formula is: (L)
Step 3: Formulate the Relationship
We assume that the centripetal force F can be expressed as:
F=k⋅ma⋅vb⋅rc
where k is a dimensionless constant and a, b, and c are the powers we need to determine.
Step 4: Write the Dimensional Formula for Force
The dimensional formula for force (F) is:
(F)=(M)(L)(T)−2
Step 5: Substitute the Dimensional Formulae
Now we substitute the dimensional formulae into the equation:
(M)(L)(T)−2=(M)a⋅(L)b⋅(L)c⋅(T)−b
This simplifies to:
(M)(L)(T)−2=(M)a⋅(L)b+c⋅(T)−b
Step 6: Equate the Powers
Now we equate the powers of each dimension on both sides:
1. For mass (M): 1=a
2. For length (L): 1=b+c
3. For time (T): −2=−b
Step 7: Solve the Equations
From the third equation, we get:
b=2
Substituting b=2 into the second equation:
1=2+c
This gives:
c=−1
Now substituting a=1, b=2, and c=−1 into our original formula:
F=k⋅m1⋅v2⋅r−1
This simplifies to:
F=k⋅mv2r
Step 8: Conclusion
Thus, the formula for centripetal force is:
F=mv2r
The centripetal force depends on three variables:
- Mass (m)
- Velocity (v)
- Radius (r)
Next, we need to write the dimensional formulae for each of these variables:
- Mass (m) has the dimensional formula: (M)
- Velocity (v) is distance per time, so its dimensional formula is: (L)(T)−1
- Radius (r) is a length, so its dimensional formula is: (L)
We assume that the centripetal force F can be expressed as:
F=k⋅ma⋅vb⋅rc
where k is a dimensionless constant and a, b, and c are the powers we need to determine.
The dimensional formula for force (F) is:
(F)=(M)(L)(T)−2
Now we substitute the dimensional formulae into the equation:
(M)(L)(T)−2=(M)a⋅(L)b⋅(L)c⋅(T)−b
(M)(L)(T)−2=(M)a⋅(L)b+c⋅(T)−b
Now we equate the powers of each dimension on both sides:
1. For mass (M): 1=a
2. For length (L): 1=b+c
3. For time (T): −2=−b
From the third equation, we get:
b=2
1=2+c
This gives:
c=−1
F=k⋅m1⋅v2⋅r−1
This simplifies to:
F=k⋅mv2r
Thus, the formula for centripetal force is:
F=mv2r
Similar Questions
The contripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and redio ( r) of the circle . Derive the formula for F using the method of dimensions.
View SolutionA body of mass m is moving in a circle of radius angular velocity ω. Find the expression for centripetal force acting on it by the method of dimensions
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a body of mass m moving with a uniform speed v along a circle of radius r . The change in velocity in going from A to B is
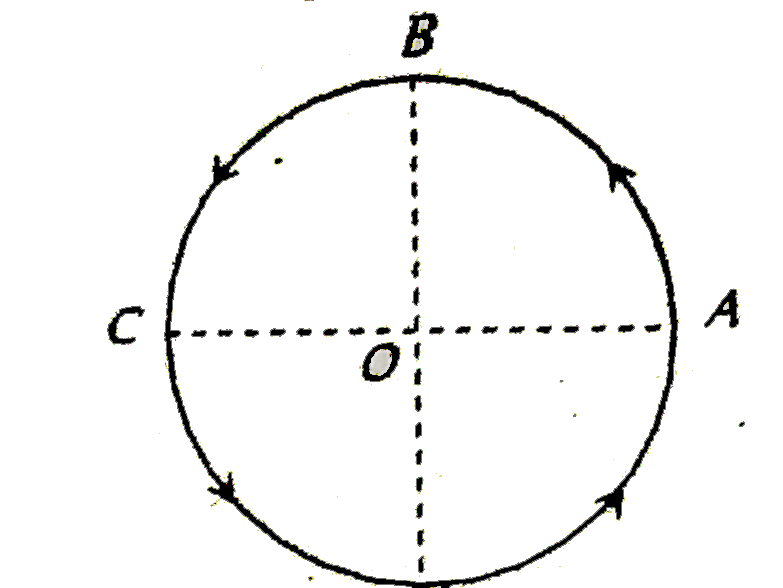 Av√2Bv/√2CvDZero
Av√2Bv/√2CvDZero - Question 2 - Select One
If a body is moving with a uniform speed v in a circle of radius 'r', then the angular acceleration of the body will be
Av/rBv2r along the radius and away from the centreCv2r along radius and toward centreDzero - Question 3 - Select One
The magnitude of the centripetal force acting on a body of mass m executing uniform motion in a circle of radius r with speed v is
AmvrBmv2/rCv/r2mDv/rm
The centripetal force acting on a body of mass m moving with speed v along a circular path of radius r is given by
F=mv2r
If the values of m , v and r are measured as 0.5 kg , 10ms−1 and 0.4 m respectively to the accuracies of 0.005 kg , 0.01ms−1 and 0.01 m respectively , calculate the percentage error in the force acting on the body.View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View SolutionThe magnitude of the centripetal force acting on a body of mass m executing uniform motion in a circle of radius r with speed v is
View SolutionA body of mass 1kg is moving with a uniform speed of 1m/s in a circular path of radius 1m. The external force acting on the body is
View SolutionA body of mass m is movinng in a circlee off radius r with a constant speed v. the work done by the centripetal force in moving the body over half the circumference of the circle is
View Solution

