Draw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
To draw a graph showing the variation of potential energy (PE), kinetic energy (KE), and total energy (TE) of a simple harmonic oscillator with displacement (x), we will follow these steps:
Step 1: Understand the equations for PE and KE
- Potential Energy (PE): The potential energy of a simple harmonic oscillator is given by the formula:
PE=12kx2
or equivalently,
PE=12mω2x2
where k is the spring constant, m is the mass, and ω is the angular frequency.
- Kinetic Energy (KE): The kinetic energy is given by:
KE=12mv2
where v is the velocity. In terms of displacement, it can be expressed as:
KE=12mω2(a2−x2)
where a is the amplitude of the oscillation.
Step 2: Determine the maximum values
- At maximum displacement (x=±a), the potential energy is maximum:
PEmax=12mω2a2
and the kinetic energy is zero:
KE=0
- At the equilibrium position (x=0), the potential energy is zero:
PE=0
and the kinetic energy is maximum:
KEmax=12mω2a2
Step 3: Total Energy (TE)
- The total energy of the system is constant and is equal to the maximum potential energy or maximum kinetic energy:
TE=12mω2a2
Step 4: Plotting the graphs
1. Draw the axes: The horizontal axis represents displacement x (from −a to +a), and the vertical axis represents energy (PE, KE, TE).
2. Plot the Potential Energy (PE):
- The graph of PE is a parabola opening upwards, starting from the origin (0,0) at x=0 and reaching its maximum at x=±a.
3. Plot the Kinetic Energy (KE):
- The graph of KE is also a parabola, but it starts from its maximum value at x=0 and decreases to zero at x=±a.
4. Plot the Total Energy (TE):
- The total energy is a horizontal line across the graph at the value of 12mω2a2, indicating that it remains constant regardless of displacement.
Final Graph Representation
- The graph will show:
- The PE curve starting from (0,0) and peaking at (±a,12mω2a2).
- The KE curve starting from (0,12mω2a2) and touching the x-axis at (±a,0).
- A horizontal line representing the TE at 12mω2a2.
- Potential Energy (PE): The potential energy of a simple harmonic oscillator is given by the formula:
PE=12kx2
or equivalently,
PE=12mω2x2
where k is the spring constant, m is the mass, and ω is the angular frequency.
KE=12mv2
where v is the velocity. In terms of displacement, it can be expressed as:
KE=12mω2(a2−x2)
where a is the amplitude of the oscillation.
- At maximum displacement (x=±a), the potential energy is maximum:
PEmax=12mω2a2
and the kinetic energy is zero:
KE=0
PE=0
and the kinetic energy is maximum:
KEmax=12mω2a2
- The total energy of the system is constant and is equal to the maximum potential energy or maximum kinetic energy:
TE=12mω2a2
1. Draw the axes: The horizontal axis represents displacement x (from −a to +a), and the vertical axis represents energy (PE, KE, TE).
2. Plot the Potential Energy (PE):
- The graph of PE is a parabola opening upwards, starting from the origin (0,0) at x=0 and reaching its maximum at x=±a.
- The graph of KE is also a parabola, but it starts from its maximum value at x=0 and decreases to zero at x=±a.
- The total energy is a horizontal line across the graph at the value of 12mω2a2, indicating that it remains constant regardless of displacement.
- The graph will show:
- The PE curve starting from (0,0) and peaking at (±a,12mω2a2).
- The KE curve starting from (0,12mω2a2) and touching the x-axis at (±a,0).
- A horizontal line representing the TE at 12mω2a2.
Topper's Solved these Questions
Similar Questions
Draw a graph to show the the variation of P.E., K.E. and total eneryg of a simple harmonic oscillator with displacement .
View SolutionA particle is executing S.H.M. along a straight line. The graph showing the variation of kinetic, potential and total energy K, U and T respectively with displacement is -
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The phase of simple harmonic oscillator is
Aexpressed in timeBexpressed in angleCexpressed in distanceDa' and 'b' - Question 2 - Select One
Simple harmonic oscillations are
Aone dimensionalBthree dimensionalCtwo dimensionalDfour dimensional - Question 3 - Select One
In a simple harmonic oscillator, at the mean position
A(a) kinetic energy is minimum, potential energy is maximum.B(b) both kinetic and potential energies are maximum.C(c ) kinetic energy is maximum, potential energy is minimum.D(d) both kinetic and potenteal energies are minimum.
Draw a graph showing the variation of decay rate with number of active nuclei.
View SolutionIn. a simple harmonic oscillator, at the mean position
View SolutionA particle is executing S.H.M. along a straight line. The graph showing the variation of kinetic, potential and total energy K, U and T respectively with displacement is -
 View Solution
View SolutionThe variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
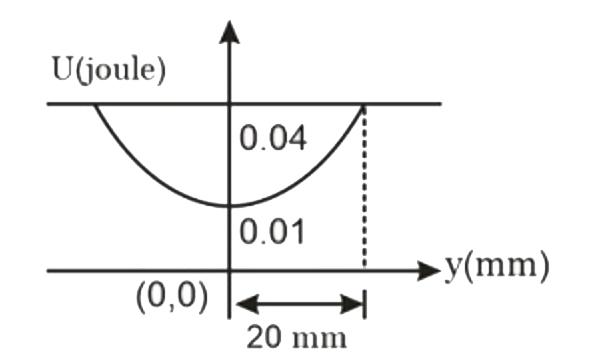 View Solution
View SolutionFrequency of variation of kinetic energy of a simple harmonic motion of frequency n is
View Solution

