If A ( 2,2,-3) B ( 5,6,9) ,C (2,7,9) be the vertices of a triangle. The internal bisector of the angle A meets BC at the point D, then find the coordinates of D.

Video Solution

Text Solution

Verified by Experts

Let the coordinates of D are (x,y,z)
$A B = \sqrt{9 + 16 + 144} = \sqrt{169} = 13$
$A C = \sqrt{0 + 25 + 144} = \sqrt{169} = \sqrt{13}$
$\frac{A B}{A C} = \frac{13}{13} \Rightarrow A B = A C$
$\frac{B D}{D C} = \frac{1}{1} \Rightarrow B D = D C$
Since, D is divide the line BC in two equal parts parts. So, D is the mid-point of BC.
$x = \frac{5 + 2}{2} = 7 / 2$
$y = \frac{6 + 7}{2} = 13 / 2$
$z = \frac{9 + 9}{2} = 9$
So, the coordinates of D are $(\frac{7}{2}, \frac{13}{2}, 9)$

|

Updated on:21/07/2023

Class 11 MATHS INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

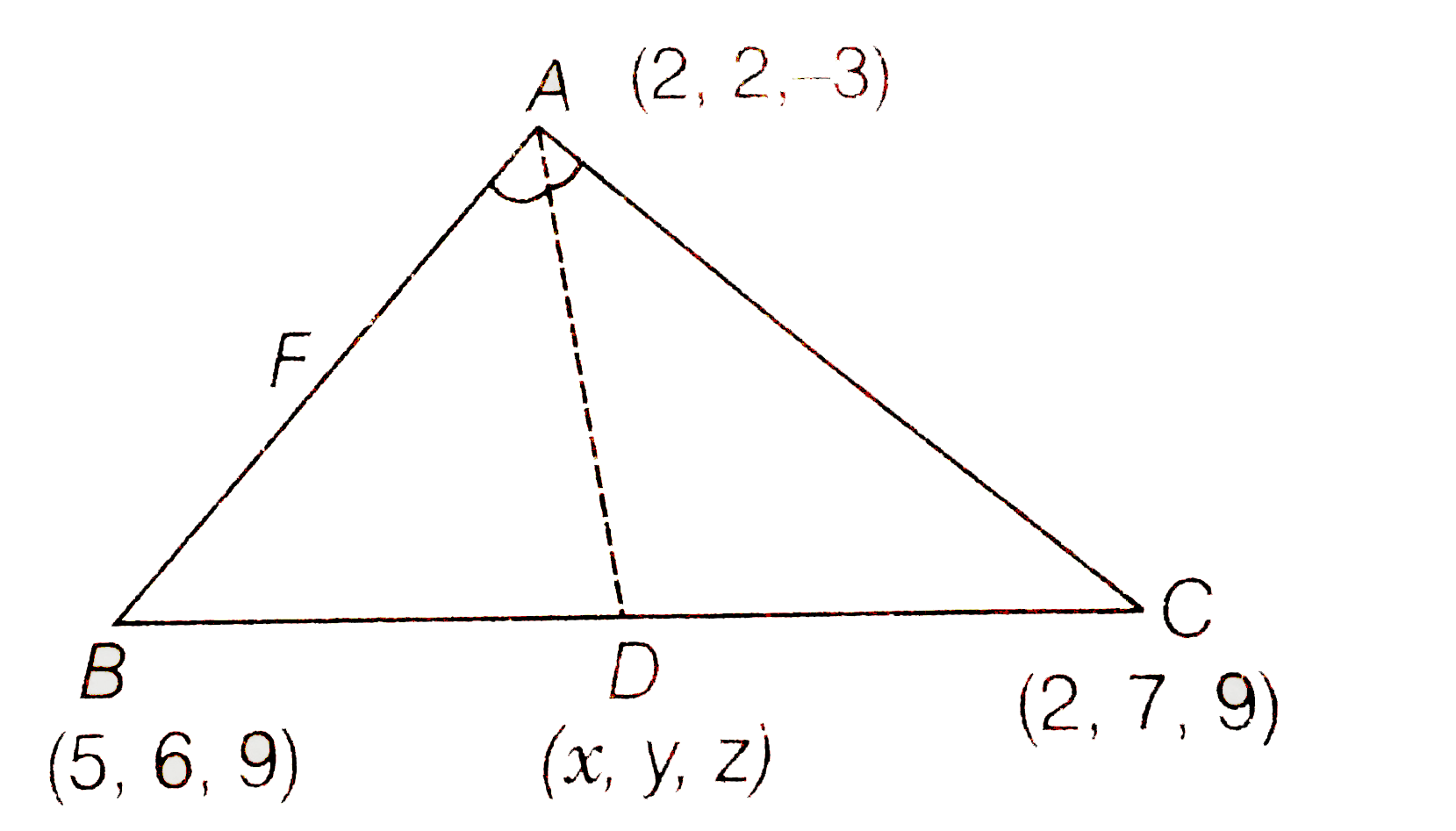
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$A (3, 2, 0), B (5, 3, 2), C (- 9, 6, - 3)$ are the vertices of a triangle ABC. If the bisector of $∠ B A C$ meets BC at D, then coordinates of D are
A $(\frac{19}{8}, \frac{57}{16}, \frac{17}{16})$
B $(- \frac{19}{8}, \frac{57}{16}, \frac{17}{16})$
C $(\frac{19}{8}, - \frac{57}{16}, \frac{17}{16})$
D $(\frac{19}{8}, \frac{57}{16}, - \frac{17}{16})$
Question 2 - Select One
$A (3, 2, 0), B (5, 3, 2) and C (- 9, 8, - 10)$ are the vertices of a triangle ABC. If the bisector of $∠ A B C$ meets BC atD, then coordinates of D are
A $(\frac{19}{8}, \frac{57}{16}, \frac{17}{16})$
B $(\frac{- 19}{8}, \frac{57}{16}, \frac{17}{16})$
C $(\frac{19}{8}, - \frac{57}{16}, \frac{17}{16})$
DNone of these
Question 3 - Select One
If A (3, 2, 0), B (5, 3, 2) and C (-9, 6, -3 ) are three points forming a triangle and AD is bisector of $∠$ BAC, then AD meets BC at the point
A $(19, 8, \frac{57}{16}, \frac{17}{16})$
B $(- \frac{19}{8}, \frac{57}{16}, \frac{17}{16})$
C $(\frac{19}{8}, \frac{57}{16}, 17, 16)$
Dnone of these

NCERT EXEMPLAR-INTRODUCTION TO THREE DIMENSIONAL GEOMETRY-Fillers

Home
Ask Doubt
Profile