Question

D and E are the mid-points of the sides AB and AC of $\Delta$ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is

Options

A. a square
B. a rectangle
C. a rhombus
D. a parallelogram

Answer

D

Explanation

In `Delta`ABC, D and E are the mid-points of sides AB and AC, respectively. ltBrgt By mid-point theorem,
`DE||BC`
and `" "DE=(1)/(2)BC" "...(i)`
Then, `" "DE=(1)/(2)[BP+PO+OQ+QC]` ltBrgt `DE=(1)/(2)[2PO+2OQ]`
`" "`[since, P and Q are the mid-points of OB and OC respectively]
`rArr" "DE=PO+OQ`
`rArr" "DE=PQ`
Now, in `Delta`AOC, Q and E are the mid-points of OC and AC respectively.

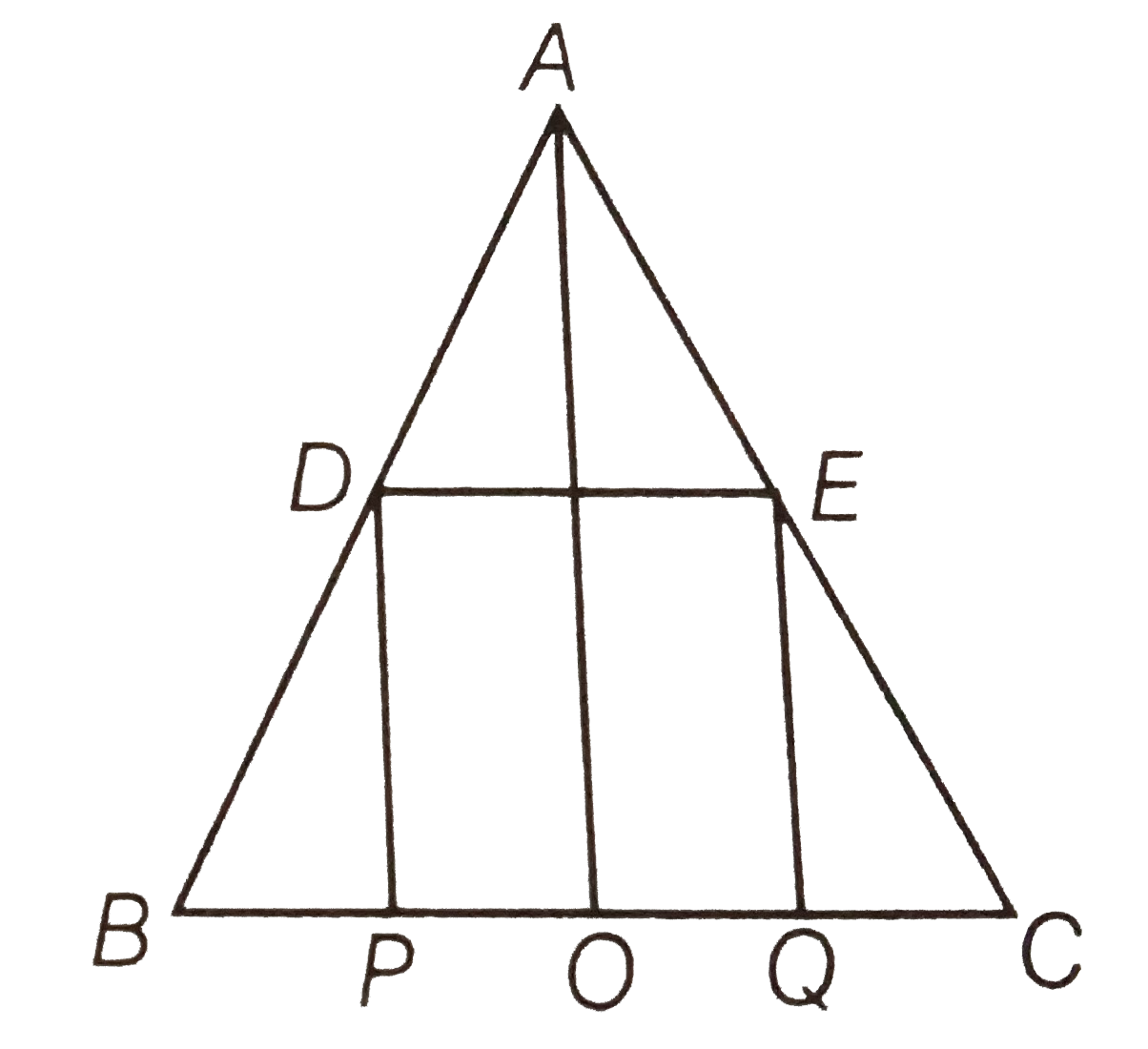
`therefore" "EQ||AO and EQ= (1)/(2)AO`
[by mid-point theorem]...(iii)
Similarly, in `Delta`ABO, PD`||`AO and PD = `(1)/(2)AO`
[by mid-point theorem]...(iv)
From Eqs. (iii) and (iv),
`EQ||PDandEQ=PD`
From Eqs. (i) and (ii), `DE||BC(or DE||PQ)andDE=PQ`
Hence, DEQP is a parallelogram.