Let T1 and T2 be the time periods of two springs A and B when a mass m is suspnded from them seperately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then -
T=T1+T2
T=T1T2T1+T2
T2=T21+T22
1T2=1T21+1T22
The correct Answer is:4
T1=2π√mk1⇒k1=4π2mT21
T2=2π√mk2⇒k2=4π2mT22
Now T=2π√Mkk=4π2mT2
in parallel k=K1+k2
Topper's Solved these Questions
Similar Questions
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
View Solution
Knowledge Check
- Question 1 - Select One
Let T1 and T2 be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
AT=T1+T2BT=T1T2T1+T2CT2=T21+T22D1T2=1T21+1T(2)2 - Question 2 - Select One
Let T1andT2 be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass A is, suspended from the séries combination, the time period is T, then
AT=T1+T2B1T=1T1+1T2CT2=T21+T22D1T2=1T21+1T2 - Question 3 - Select One
The time period of a mass suspended from a spring is T if the spring is cut in to equal part and the same mass is suspended from one of the pert then the time period will be
ATBT2C2TDT4
A block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionThe time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:
View SolutionFind the ratio of the periods of two identical springs if they are first joined in series & then in parallel & a mass m is suspended from them:
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
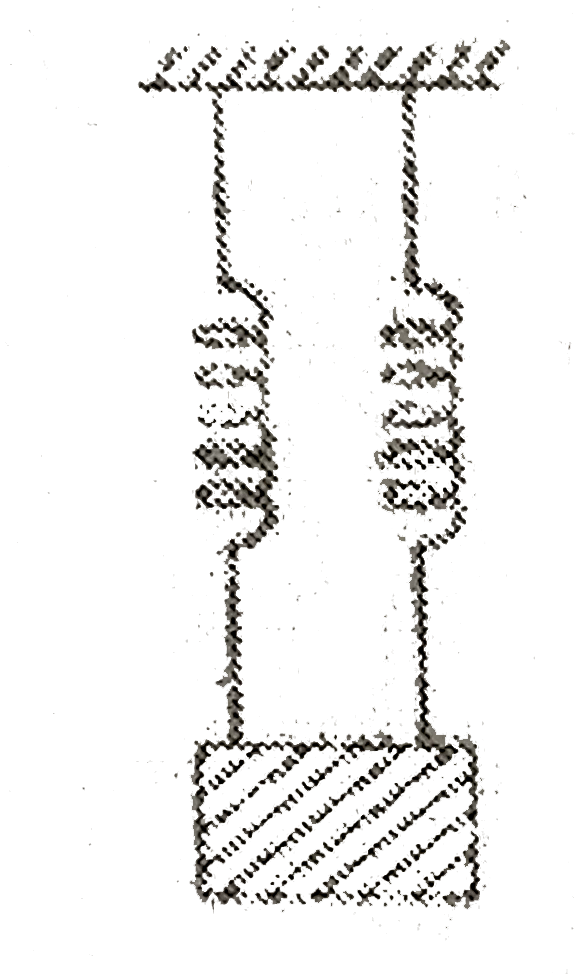 View Solution
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspsended with two halves as shown in figure. The new time period of oscillation will become
 View Solution
View Solution

