In the figure given below, the end B of the rod AB which makes angle θ with the floor is pulled with a constant velocity v0 as shown. The length of rod is l. At an instant when θ=37∘
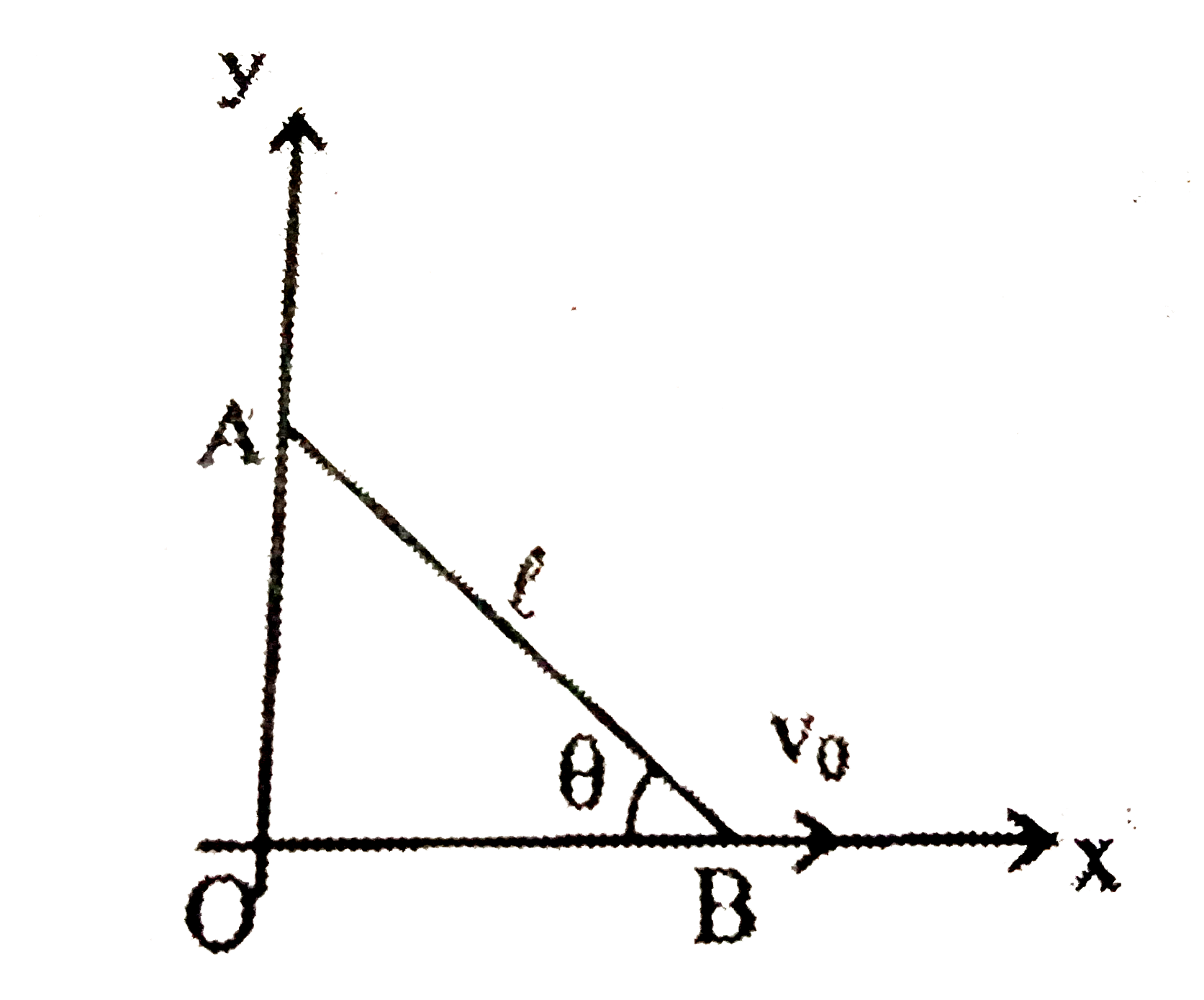
Velocity of end A is 4v03
angular velocity of rod is 5v06l
angular velocity of rod is constant
velocity of end a is constant
The correct Answer is:1
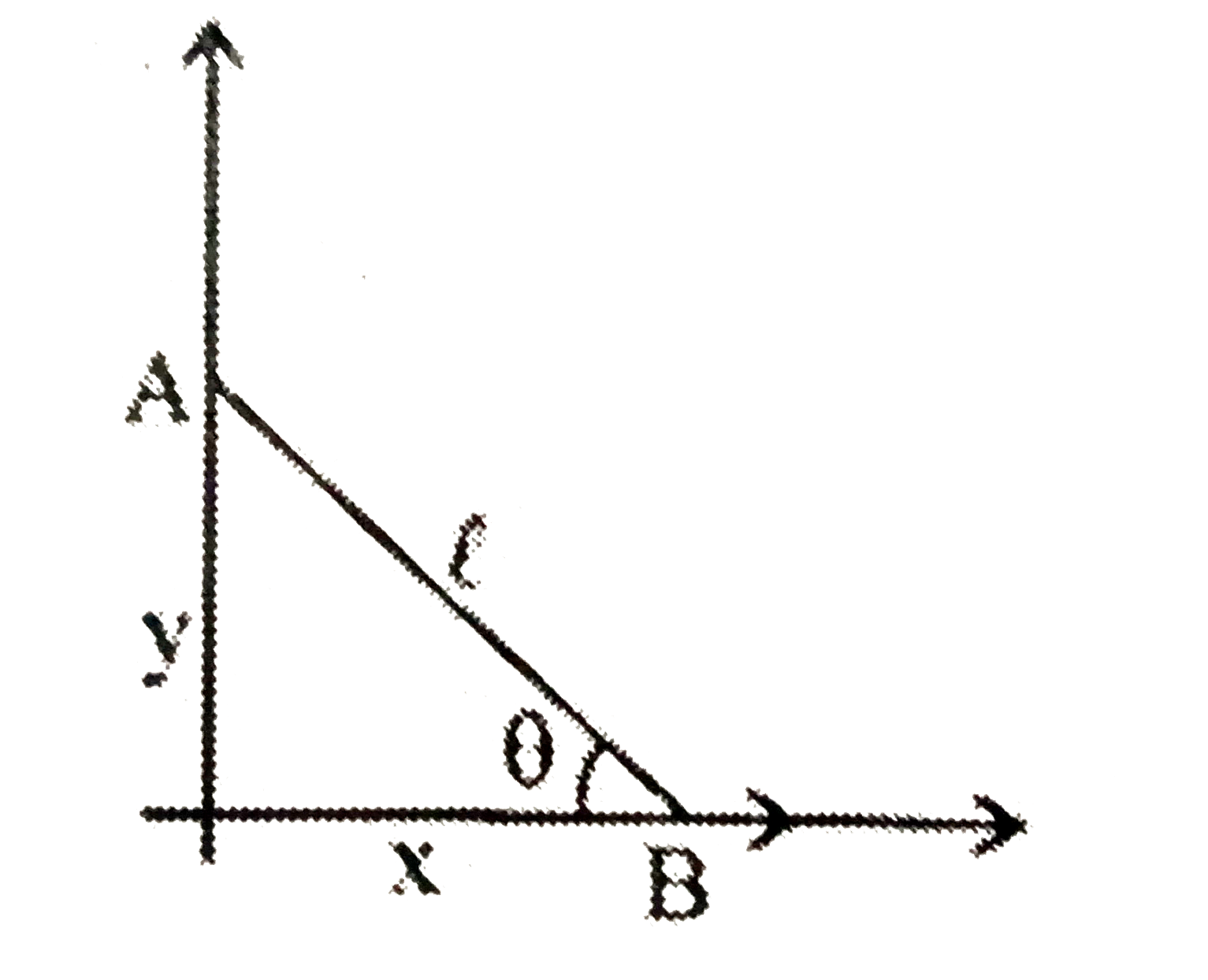
x2+y2=l2
⇒dydt=−(xy)dxdt
∴vA=−43v0
Now, x=lcosθ
dxdt=−lsinθdθdt⇒ω=−53(v0l)
Topper's Solved these Questions
Similar Questions
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘, the angular velocity of the rod is pqv0l. Find (p+q).
'(##CEN_KSR_PHY_JEE_C07_009_Q05##) '
View SolutionThe lower end of a 4 m long uniform rod AB is pulled with constant speed v=4 m/s. The speed of centre of mass of the rod at θ=60∘ will be

View Solution
Knowledge Check
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
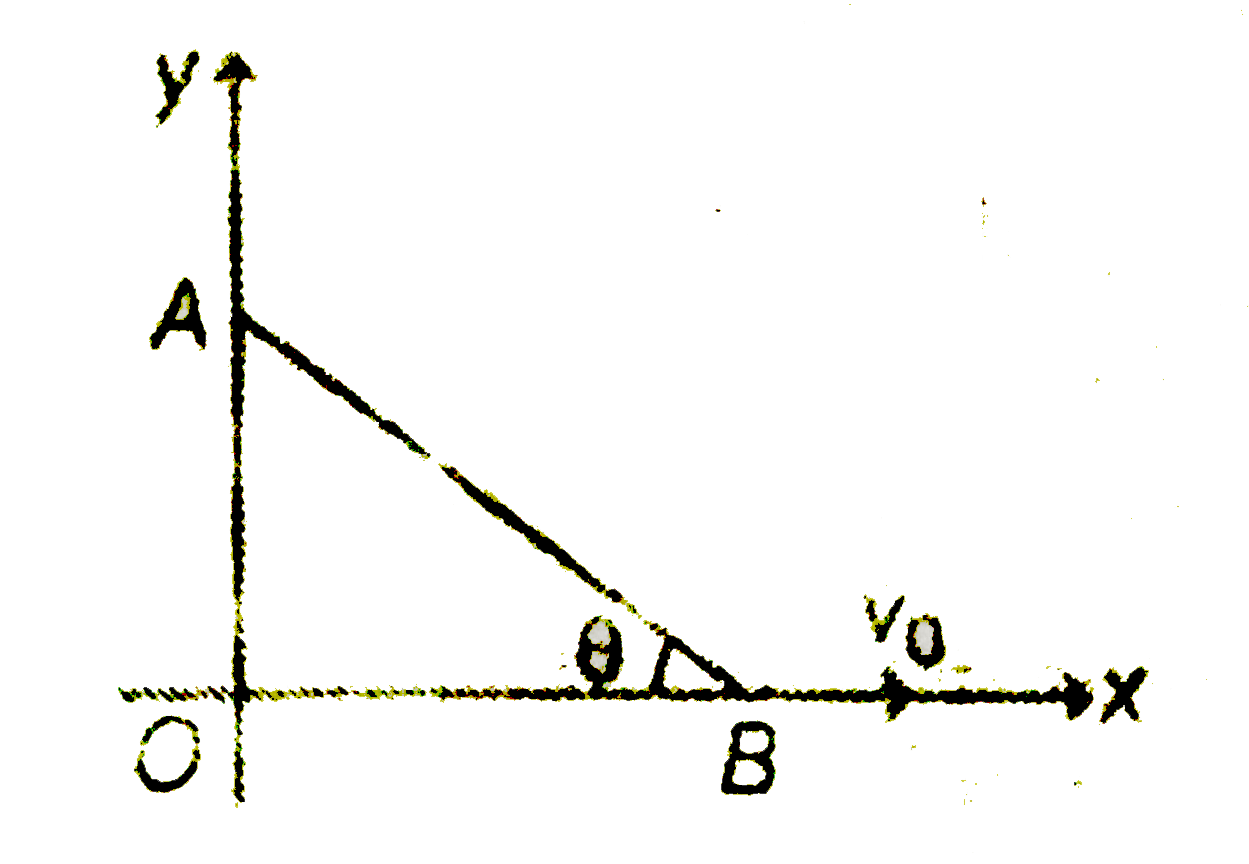 Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant
Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant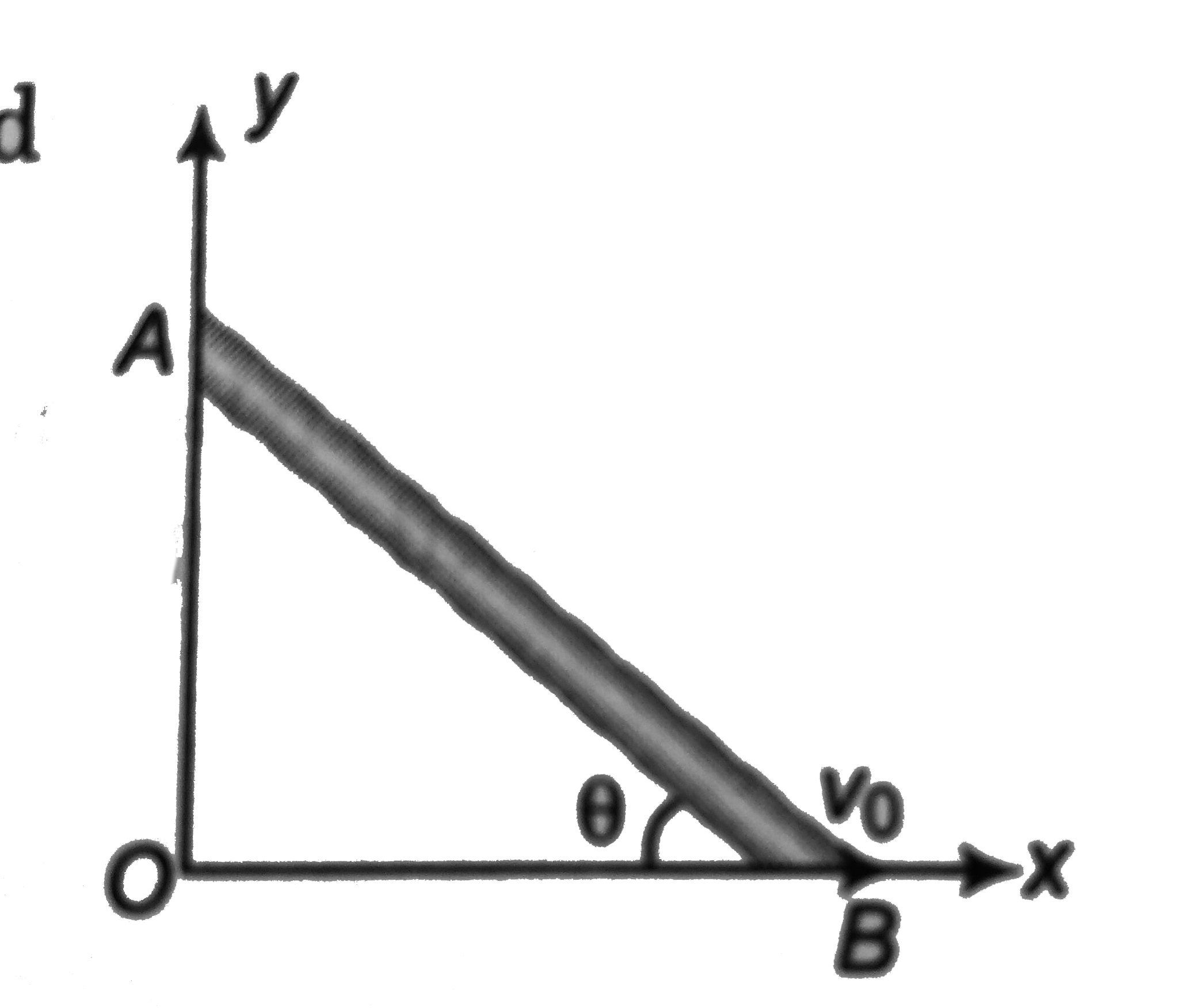
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.End A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontal
A rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod AB of length L slides in the XY plane. If the rod makes an angle θ with the vertical, the angular velocity of the rod can be found by an expression which is

View Solution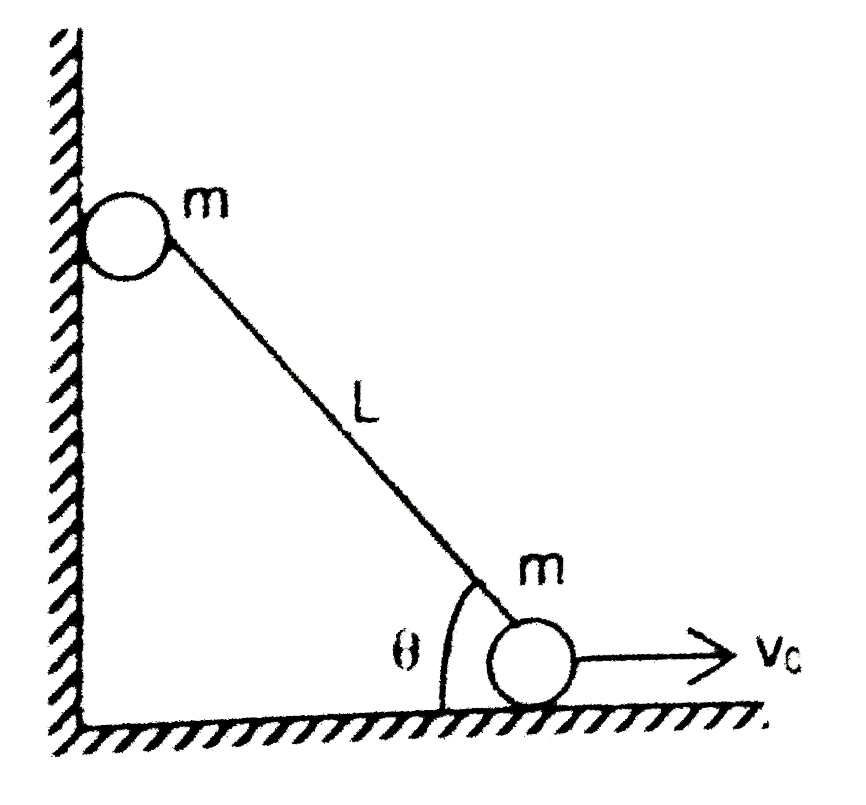
In the shown diagram two point masses m are joined by a massless rod of length 5.5m. The lower end of the mass sytem is dragged with constant velocity V0 rightwards the magnitude of velocity of centre of mass when θ=370, will be
View SolutionA rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
View Solution
