Find the image of the line x−12=y+1−1=z−34 in the plane 3x−3y+10z−26=0.
A
x−5/29=y−1/2−1=z−2−3
B
x+5/29=y+1/2−1=z+2−3
C
x−5/29=y+1/2−1=z+2−3
D
None of these
Video Solution
Text Solution
The correct Answer is:1
x−19=y−2−1=z+3−3=1 .......(1)
3x−3y+10z−26=0 ......(2)
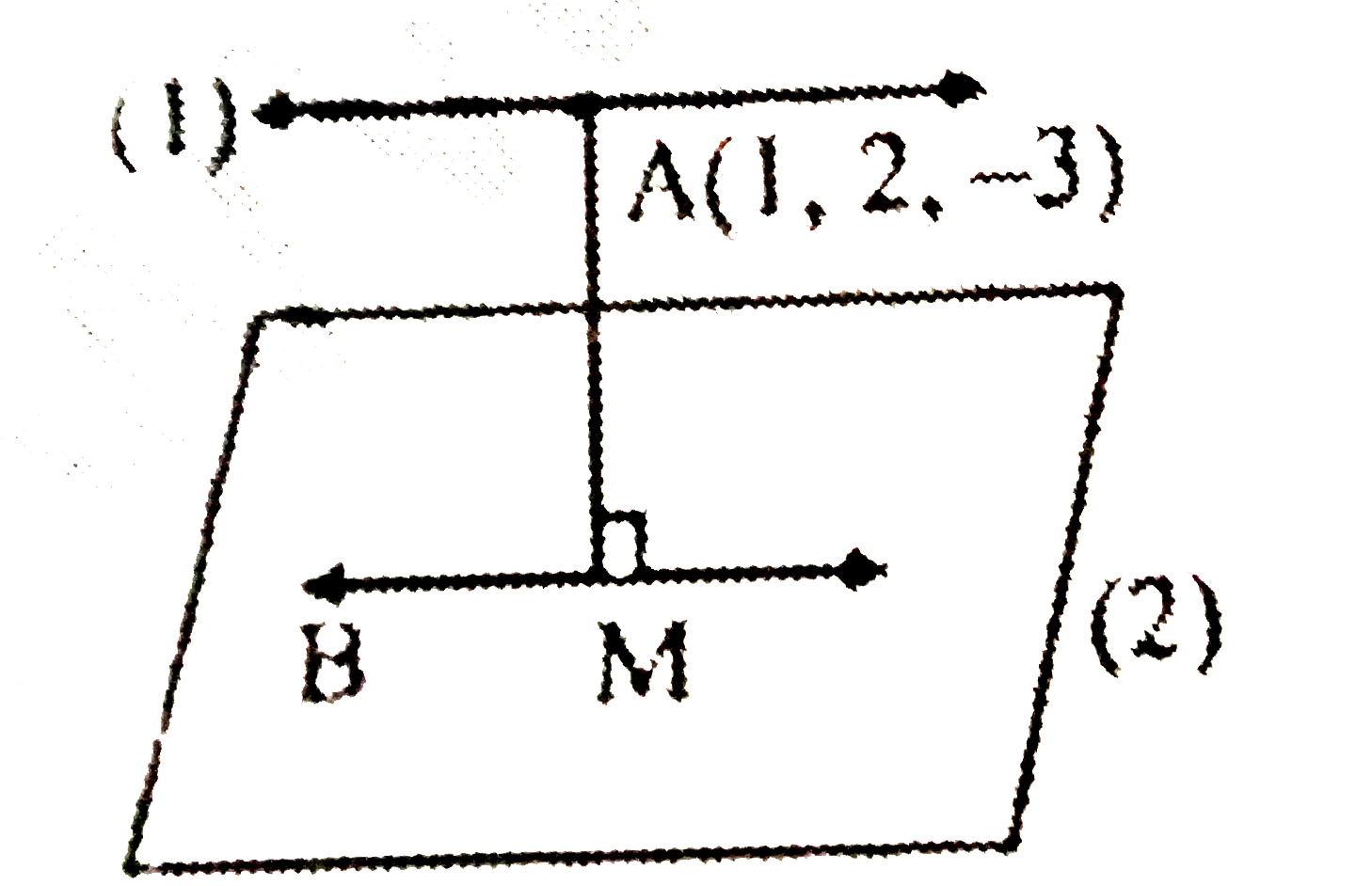
point M is the image of point A in plane (2)
(i.e . Foot of the perpendicular )
∴ (DR's of the normal of the plane (2))--(DR's of the line AM )=3,-310
then equation of line
AM⇒x−13=y−2−3=z+310=λ
M(x1,y1,z1)=(3λ+1,−3λ+2,10λ−3)
∵point M lies in the plane (2)
then3x1−3y1+10z1−26=0
3(3λ+1)−3(−3λ+2)+10(10λ−3)−26=0
118λ=59⇒λ=1/2
∴M{52,12,2}
∴ equation of line B M
⇒(x−52)9=(y−12)−1=(z−2)−3
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The image of the line x−22=y−3−3=z−41 in the plane x+y+z=6 can be
A→r=λ(2ˆi−3ˆj+ˆk)B→r=(2ˆi+ˆj+ˆk)+α(2ˆi−3ˆj+ˆk)C→r=(ˆj+2ˆk)+β(2ˆi−3ˆj+ˆk)D→r=(ˆi+2ˆj)+u(2ˆi−3ˆj+ˆk)The image of the line x−13=y−31=z−4−5 in the plane 2x−y+z+3=0 is the line (1) x+33=y−51=z−2−5 (2) x+3−3=y−5−1=z+25 (3) x−33=y+51=z−2−5 (3) x−3−3=y+5−1=z−25
Ax−3−3=y+5−1=z−25Bx+33=y−51=z−2−5Cx+3−3=y−5−1=z+25Dx−33=y+51=z−2−5The image of the line x−13=y−31=z−4−5 in the plane 2x−y+z+3=0 is the line (1) x+33=y−51=z−2−5 (2) x+3−3=y−5−1=z+25 (3) x−33=y+51=z−2−5 (3) x−3−3=y+5−1=z−25
Ax+33=y−51=z−2−5Bx+3−3=y−5−1=z−25Cx−33=y+51=z−2−5Dx−3−3=y+5−1=z−25
Find the equation of the projection of the line x−12=y+1−1=z−34 on the plane x+2y+z=9.
View SolutionFind the angle between the line x−13=y−12=z−14 and the plane 2x+y−3z+4=0.
View SolutionFind the angle between the line x−23=y+1−1=z−32 and the plane 3x+4y+z+5=0.
View SolutionFind the angle between the line x+12=y3=z−36and the plane 10x+2y−11z=3.
View SolutionThe image of the line x−13=y−31=z−4−5 in the plane 2x−y+z+3=0 is the line (1) x+33=y−51=z−2−5 (2) x+3−3=y−5−1=z+25 (3) x−33=y+51=z−2−5 (3) x−3−3=y+5−1=z−25
View Solution