Through the centriod of an equilateral triangle a line parallel to the base is drawn. On this line, an arbitary point P is taken inside the triangle. Let h denote the distahce of P from the base of the triangle. Let $h_{1} and h_{2}$ be the distance of P from the other two sides of the triangle, then

A

h is the H.M of $h_{1}, h_{2}$

B

h is the G.M of $h_{1}, h_{2}$

C

h is the A.M of $h_{1}, h_{2}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

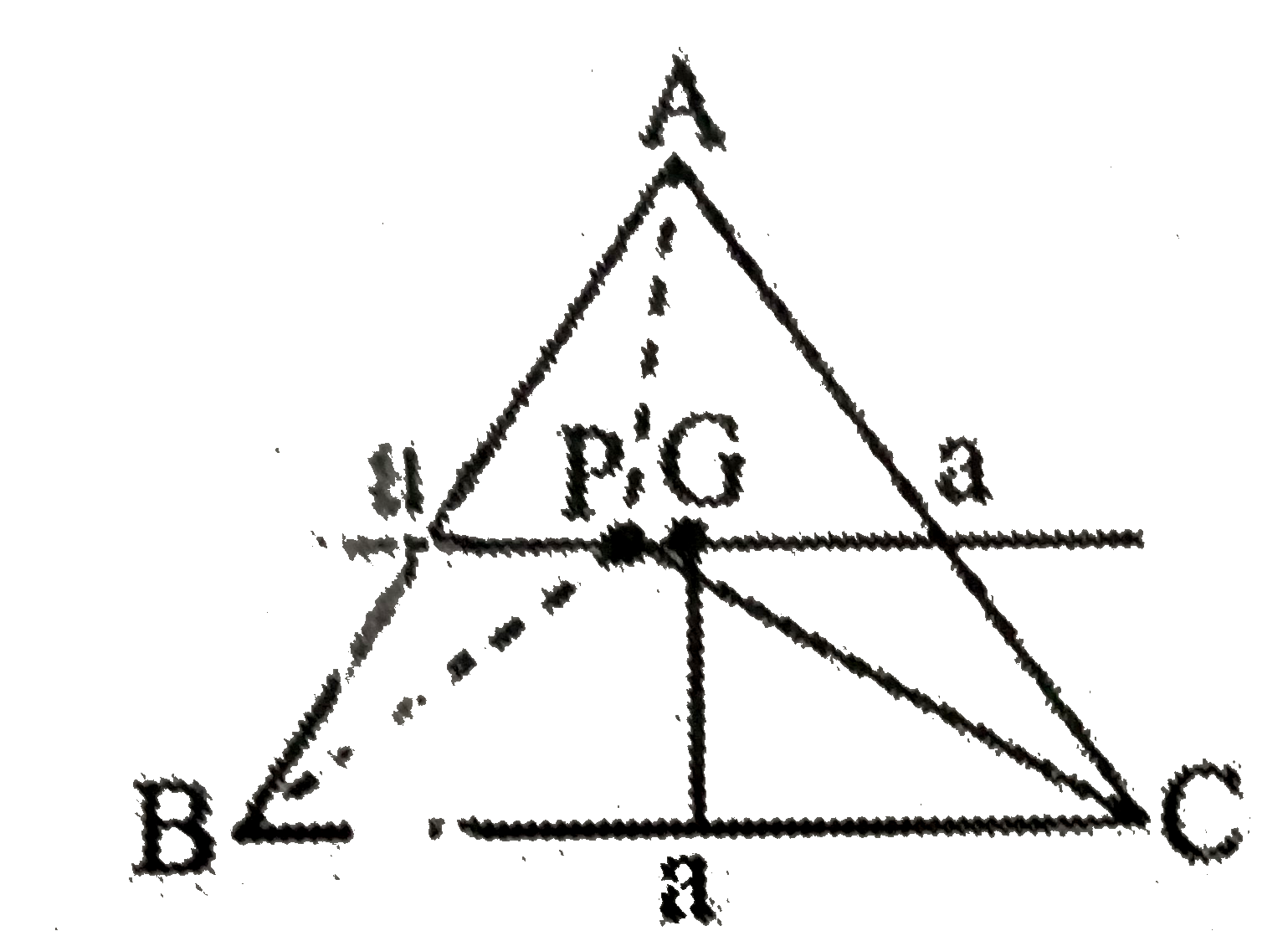
$Δ A B C = Δ P A B + Δ P B C + Δ P A C$
$\frac{1}{2} \times a \times (3 h) = \frac{1}{2} a h_{1} + \frac{1}{2} a h + \frac{1}{2} a h_{2}$
$\Rightarrow h = \frac{h_{1} + h_{2}}{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

BOOK - CAREER POINTCHAPTER - MOCK TEST 8EXERCISE - PART (C ) - MATHS
30videos
MOCK TEST 8

Similar Questions

Knowledge Check

Question 1 - Select One
Through the centroid of an equilateral triangle, a line parallel to the base is drawn. On this line, an arbitrary point P is taken inside the triangle. Let h denote the perpendicular distance of P from the base of the triangle. Let $h_{1} and h_{2}$ be the perpendicular distance of P from the other two sides of the triangle . Then :
A $h = \frac{h_{1} + h_{2}}{2}$
B $h = \sqrt{h_{1} h_{2}}$
C $h = \frac{2 h_{1} h_{2}}{h_{1} + h_{2}}$
D $h = \frac{(h_{1} + h_{2}) \sqrt{3}}{4}$
Question 2 - Select One
A point P lying inside a triangle is equidistant from the vertices of the triangle. Then the triangle has P as its
ACentroid
BIncentre
COrthocentre
DCircumcentre
Question 3 - Select One
A point O is inside an equilateral triangle, if the distance of O from the sides are $\sqrt{12}, \sqrt{27} and \sqrt{48}$ , then the length of the side of the triangle, is
A $10 \sqrt{3}$
B $15 \sqrt{3}$
C18
D20

CAREER POINT-MOCK TEST 9-MATHS

Home
Ask Doubt
Profile