Find the radius of the smallest circular disk large enough to cover every isosceles triangle of a given perimeter L.
To find the radius of the smallest circular disk large enough to cover every isosceles triangle of a given perimeter L, we can follow these steps:
Step 1: Define the Triangle
Let the isosceles triangle have two equal sides AB=AC=a and the base BC=b. The perimeter L is given by:
L=2a+b
Step 2: Express Base in Terms of a
From the perimeter equation, we can express b in terms of a:
b=L−2a
Step 3: Relate Triangle Dimensions to Circle Radius
The radius R of the circumcircle of a triangle can be expressed in terms of its sides and the angle θ at vertex A (where AB and AC meet):
R=a2sin(θ)
Step 4: Use the Law of Cosines
To find θ, we can use the law of cosines. The length of the base b can also be expressed in terms of a and θ:
b2=a2+a2−2a2cos(θ)=2a2(1−cos(θ))
Step 5: Express R in Terms of L
Substituting b=L−2a into the equation gives:
(L−2a)2=2a2(1−cos(θ))
Step 6: Find the Area of the Triangle
The area A of the triangle can be expressed as:
A=12×b×h
where h is the height from vertex A to base BC. The height can be expressed in terms of R and θ:
h=Rsin(θ)
Step 7: Set Up the Equation for Minimization
To find the minimum radius R, we need to minimize the area A or the radius R with respect to θ. We can express the area in terms of R and θ.
Step 8: Differentiate and Solve for Critical Points
To find the minimum, we differentiate the area with respect to θ and set it to zero:
dAdθ=0
Step 9: Solve for θ
This will give us the critical points for θ. We can then find the corresponding R.
Step 10: Substitute Back to Find R
After finding θ, substitute back to find the radius R:
R=L2(0.68+√2⋅1.732)
Final Result
After evaluating the above expression, we find:
R=0.196L
Let the isosceles triangle have two equal sides AB=AC=a and the base BC=b. The perimeter L is given by:
L=2a+b
From the perimeter equation, we can express b in terms of a:
b=L−2a
The radius R of the circumcircle of a triangle can be expressed in terms of its sides and the angle θ at vertex A (where AB and AC meet):
R=a2sin(θ)
To find θ, we can use the law of cosines. The length of the base b can also be expressed in terms of a and θ:
b2=a2+a2−2a2cos(θ)=2a2(1−cos(θ))
Substituting b=L−2a into the equation gives:
(L−2a)2=2a2(1−cos(θ))
The area A of the triangle can be expressed as:
A=12×b×h
where h is the height from vertex A to base BC. The height can be expressed in terms of R and θ:
h=Rsin(θ)
To find the minimum radius R, we need to minimize the area A or the radius R with respect to θ. We can express the area in terms of R and θ.
To find the minimum, we differentiate the area with respect to θ and set it to zero:
dAdθ=0
This will give us the critical points for θ. We can then find the corresponding R.
After finding θ, substitute back to find the radius R:
R=L2(0.68+√2⋅1.732)
After evaluating the above expression, we find:
R=0.196L
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE -1 (SECTION - A)
7 Videos
- MAXIMA AND MINIMA BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE -1 (SECTION -B)
16 Videos
- MATRICES BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)
28 Videos
- METHOD OF DIFFERENTIATIONBOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 4 LEVEL -II
5 Videos
Similar Questions
Find in-radius for the given triangle
View SolutionA circular disk of unit radius is filled with a number of smaller circular disks arranged in the form of hexagon. Let An denotes a stack of disks arranged in the shape of a hexagon having 'n' disks on a side. The figure shows the configuration A3. If A be the area of large disk, Sn be the number of disks in An configuration and rn be the radius of each disk in An configuration, then limn→∞Snn2 limn→∞nrn
View Solution
Knowledge Check
The figure below is made up of an isosceles triangle and a semicircle. Find the perimeter of the figure.
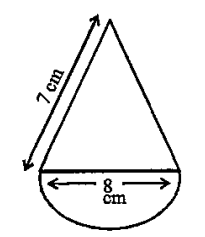 A7(4π)cmB2(2+7π)cmC2(7+2π)cmD14πcm
A7(4π)cmB2(2+7π)cmC2(7+2π)cmD14πcmFind the area of the shaded region in the diagram below where the given triangle is isosceles with vertices of base lying on axis of the radius perpendicular to the diameters of the two small semicircles
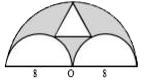 A8+16√2B16−√2C16(π−1)D16π
A8+16√2B16−√2C16(π−1)D16πIf the perimeter of a square is 80 cm, then what is the diagonal of the square (in cm) ?
A10+4√5cmB12+5√5cmC16 cmD14+4√5 cm
Find the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View SolutionFind the area of a figure formed by a square of side 8 cm and an isosceles triangle with base as one side of the square and perimeter as 18 cm.
View SolutionArea of an isosceles triangle is 48cm2. If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.
View SolutionThe base of an isosceles triangle is 12 cm and its perimeter is 32 cm. Find its area.
View SolutionFind the number of all integer-sided isosceles obtuse-angled triangles with perimeter 2008.
View Solution
