The lower corner of a leaf in a book is folded over so as to reach the inner edge of the page. Show that the fraction of the width folded over when the area of the folded part is minimum is 2/3.
5/8
2/3
3/4
4/5
The correct Answer is:B
Step by step video, text & image solution for The lower corner of a leaf in a book is folded over so as to reach the inner edge of the page. Show that the fraction of the width folded over when the area of the folded part is minimum is 2//3. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE - 2 (LEVEL - II)15videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE - 332videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE -1 (SECTION- F )2videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)28videos
MATRICES
- BOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 4 LEVEL -II5videos
METHOD OF DIFFERENTIATION
Similar Questions
If a leaf of a book is folded so that one corner moves along an opposite side, then prove that the line of crease will always touch parabola.
View SolutionA note book is made up of sheets folded in the middle and stapled. Each sheet form two leaves i.e., four pages. On removing some papers of the first half and second half of the book, Joe found the number of the leaves, in the first case as odd and in the second case as even. If the sum of the numbers of the pages on the last leaf of the book is 63, then what could be the maximum possible sum of the numbers on the pages of leaves that were left in the book.
View Solution
Knowledge Check
- Question 1 - Select One
A note book is made up of sheets folded in the middle and stapled. Each sheet form two leaves i.e., four pages. On removing some papers of the first half and second half of the book, Joe found the number of the leaves, in the first case as odd and in the second case as even. If the sum of the numbers of the pages on the last leaf of the book is 63, then what could be the maximum possible sum of the numbers on the pages of leaves that were left in the book.
A435B420C451D471 - Question 2 - Select One
The length and breadth of a rectangular sheet of a paper are 50 cm and 30 cm, respectively. A square of side 5 cm is cut and removed form the four corners of the sheet, and the rest of the pater is folded to form a cuboid (without the top face). Find the edge of the cube whose volume is one-fourth the volume of the cuboid so formed.
A12 cmB10 cmC14 cmD16 cm - Question 3 - Select One
Three atoms A, B and C crystallize in a cubic solid lattice where A atoms are present at the body centre, B atoms are present at the edge centre as well as at the corners of the cube and C atoms are present at the face centres of the cube. Now if all the atoms are removed from the two 4-fold axis and the one 2-fold axis passing through the cube, then the formula of the compound is
AB7C2BAB2C7CABC2DA5C2
The length and breadth of a rectangular sheet of a paper are 50 cm and 30 cm, respectively. A square of side 5 cm is cut and removed form the four corners of the sheet, and the rest of the pater is folded to form a cuboid (without the top face). Find the edge of the cube whose volume is one-fourth the volume of the cuboid so formed.
View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u.

(a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u/3.
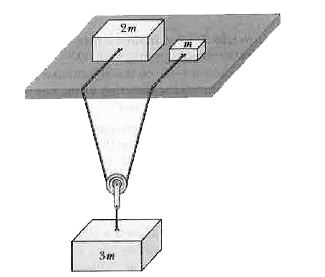
(b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).View SolutionTwo particles of masses m and 2m are placed on a smooth horizonttal table. A string, which joins these two masses, hangs over the edge supporting a pulley, which suspends a particle of mass 3m, as shown in Fig. 5-40. The pulley has negligible mass. The two parts of the string on the table are parallel and perpendicular to the edge of the table. The hanging parts of the string are vertical. Find the acceleration of the particle of mass 3m.
 View Solution
View SolutionA circular metallic sheet is divided into two parts in such away that each part can be folded in to a cone. If the ratio of their curved surface areas is 1:2, then the ratio of their volumes is
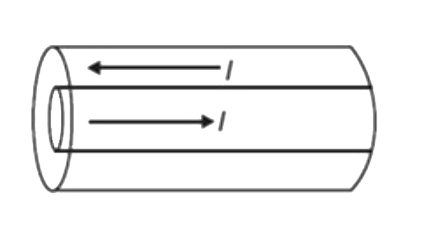
View SolutionThe figure shows a long coaxial cable in which a current I flows down through the inner cylinder of radius a and the same current flows back up through the outer cylinder of radius 2a. The cylinders are insulated from each other and the current is uniformly distributed over the area of the cross-section in each cylinder. The strength of the magnetic field at a distance 3a/2 from the axis of the cable is
 View Solution
View Solution

