A trapezium ABCD is inscribed into a semicircle of radius l so that the base AD of the trapezium is a diameter and the vertices B & C lie on the circumference. Find the base angle θ of the trapezium ABCD which has the greatest perimeter.
The correct Answer is:θ=60∘
To find the base angle θ of the trapezium ABCD that has the greatest perimeter when inscribed in a semicircle of radius l, we can follow these steps:
Step 1: Understanding the Geometry
The trapezium ABCD is inscribed in a semicircle with AD as the diameter. The points B and C lie on the circumference of the semicircle. The angle θ is the base angle at points A and D.
Step 2: Setting Up the Problem
Let the radius of the semicircle be l. The coordinates of points can be defined as follows:
- A(−l,0)
- D(l,0)
- The coordinates of points B and C can be expressed in terms of θ.
Step 3: Finding Coordinates of Points B and C
Using trigonometric identities:
- The height from points B and C to the base AD is lsinθ.
- The horizontal distances from the center to points B and C can be expressed as lcosθ.
Thus, the coordinates of B and C are:
- B(−lcosθ,lsinθ)
- C(lcosθ,lsinθ)
Step 4: Calculating the Perimeter
The perimeter P of trapezium ABCD can be calculated as:
P=AB+BC+CD+DA
Where:
- AB=√((−lcosθ)−(−l))2+(lsinθ−0)2=√l2(cosθ−1)2+l2sin2θ=l√2−2cosθ=l⋅2sin(θ2)
- CD=2lcosθ
- DA=2l
Thus, the perimeter becomes:
P=2lsin(θ2)+2lcosθ+2l
Step 5: Simplifying the Perimeter Expression
Combining the terms, we can express the perimeter as:
P=2l(1+cosθ+sin(θ2))
Step 6: Finding the Maximum Perimeter
To find the maximum perimeter, we differentiate P with respect to θ and set the derivative to zero:
dPdθ=0
Step 7: Solving the Derivative
After differentiating and simplifying, we find:
sinθ(2cosθ−1)=0
This gives us two cases:
1. sinθ=0 (which gives angles 0 or π)
2. 2cosθ−1=0 leading to cosθ=12 which gives θ=π3 or 60∘.
Step 8: Confirming Maximum
To confirm that this value gives a maximum, we can check the second derivative or evaluate the perimeter at this angle.
Final Answer
Thus, the base angle θ of the trapezium ABCD which has the greatest perimeter is:
θ=60∘orπ3 radians
The trapezium ABCD is inscribed in a semicircle with AD as the diameter. The points B and C lie on the circumference of the semicircle. The angle θ is the base angle at points A and D.
Let the radius of the semicircle be l. The coordinates of points can be defined as follows:
- A(−l,0)
- D(l,0)
- The coordinates of points B and C can be expressed in terms of θ.
Using trigonometric identities:
- The height from points B and C to the base AD is lsinθ.
- The horizontal distances from the center to points B and C can be expressed as lcosθ.
- B(−lcosθ,lsinθ)
- C(lcosθ,lsinθ)
The perimeter P of trapezium ABCD can be calculated as:
P=AB+BC+CD+DA
Where:
- AB=√((−lcosθ)−(−l))2+(lsinθ−0)2=√l2(cosθ−1)2+l2sin2θ=l√2−2cosθ=l⋅2sin(θ2)
- CD=2lcosθ
- DA=2l
P=2lsin(θ2)+2lcosθ+2l
Combining the terms, we can express the perimeter as:
P=2l(1+cosθ+sin(θ2))
To find the maximum perimeter, we differentiate P with respect to θ and set the derivative to zero:
dPdθ=0
After differentiating and simplifying, we find:
sinθ(2cosθ−1)=0
This gives us two cases:
1. sinθ=0 (which gives angles 0 or π)
2. 2cosθ−1=0 leading to cosθ=12 which gives θ=π3 or 60∘.
To confirm that this value gives a maximum, we can check the second derivative or evaluate the perimeter at this angle.
Thus, the base angle θ of the trapezium ABCD which has the greatest perimeter is:
θ=60∘orπ3 radians
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE -4 (LEVEL - I)10videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE - 4 (LEVEL - II)17videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MAXIMA AND MINIMA EXERCISE - EXERCISE - 2 (LEVEL - II)15videos
MAXIMA AND MINIMA
- BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)28videos
MATRICES
- BOOK - MOTIONCHAPTER - METHOD OF DIFFERENTIATIONEXERCISE - EXERCISE - 4 LEVEL -II5videos
METHOD OF DIFFERENTIATION
Similar Questions
A circle is inscribed in a trapezium in which one of the non-parallel sides is perpendicular to the two parallel sides. Then A) the diameter of the inscribed circle is the geometric mean of the lengths of the parallel sides B) the diameter of the inscribed circle is the harmonic mean of the lengths of the parallel sides C) the area of the trapezium is the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium D) the area of the trapezium is half the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium
View SolutionABCD is a trapezium such that AB||CD, ∠A : ∠D = 2 :1, ∠B : ∠C = 7 : 5. Find the angles of the trapezium.
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
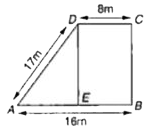 A140m2B168m2C180m2D156.4m2
A140m2B168m2C180m2D156.4m2 - Question 2 - Select One
In an isosceles trapezium ABCD, ∠C is equal to:
 A115∘B65∘C105∘D75∘
A115∘B65∘C105∘D75∘ - Question 3 - Select One
In the given pattern, eight isosceles trapeziums surround a regular octagon. The measure of ∠B in the trapezium ABCD is :
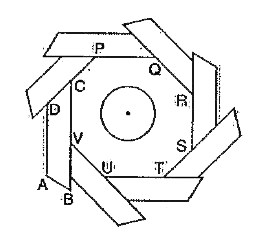 A55∘B40∘C45∘D60∘
A55∘B40∘C45∘D60∘
A current I=√2 A flows in a circuit having the shape of isosceles trapezium. The ratio of the bases of the trapezium is 2. Find the magnetic induction B at symmetric point O in the plane of the trapezium. The length of the smaller base of the trapezium is 100mm and the distance r=50mm.
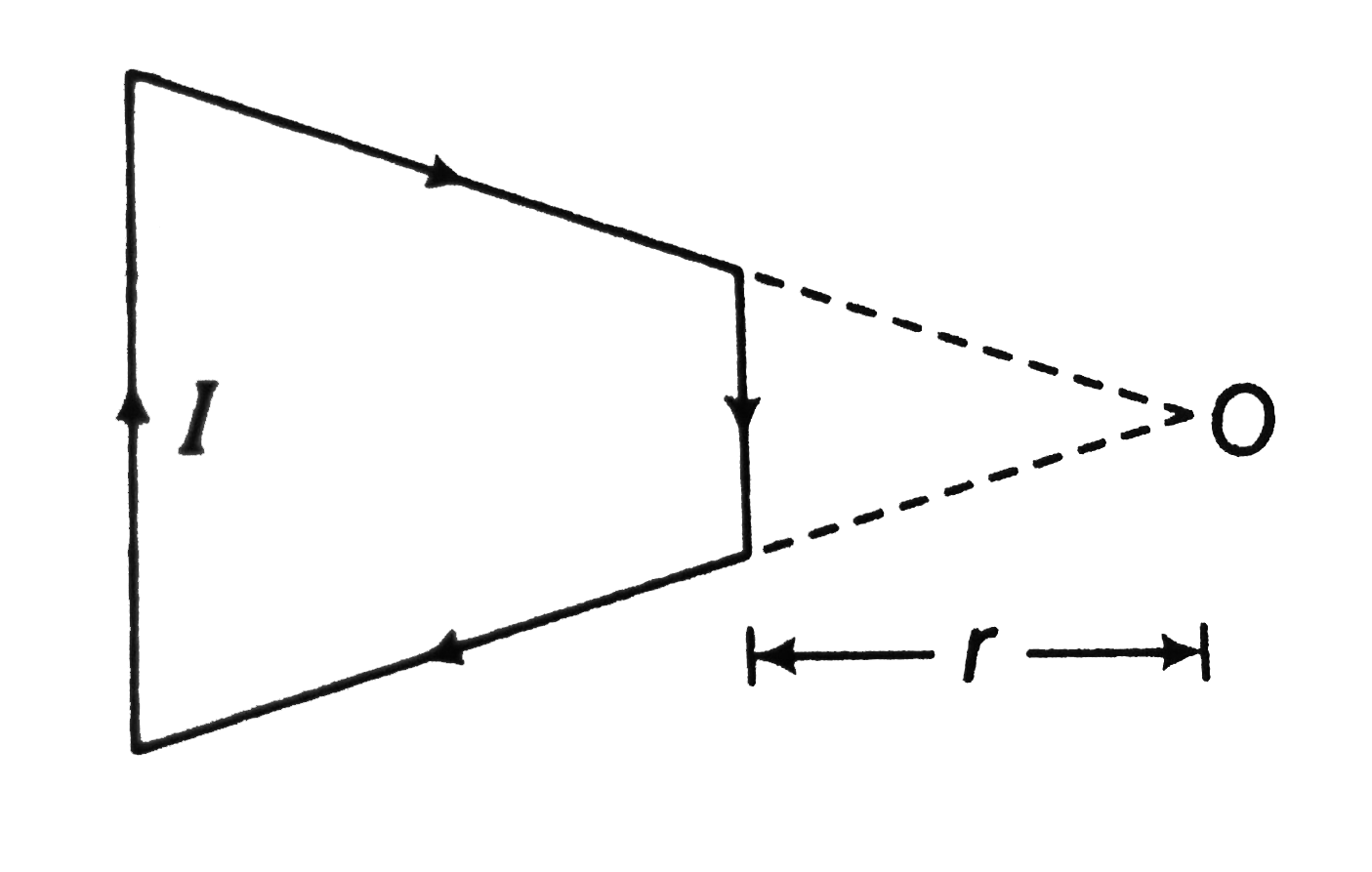 View Solution
View SolutionABCD is a cyclic trapezium with ADBC. If ∠B=700, determine other three angles of the trapezium.
View SolutionABCD is a trapezium in which AB || DC, ABデ78 cm, CD = 52 cm. AD = 28 cm and BC =30cm . Find the area of the trapezium.
View SolutionA right angled trapezium is circumscribed about a circle. Find the radius of the circle. If the lengtyhs of the bases (i.e.parallel sides ) are equal to a and b.
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View Solution

