A ray of light passes throught a plane glass slab of thickness t and refractive index μ=1.5. The angle between incident ray and emergent ray will be
0∘
30∘
45∘
60∘
The correct Answer is:A
Step by step video, text & image solution for A ray of light passes throught a plane glass slab of thickness t and refractive index mu = 1.5 . The angle between incident ray and emergent ray will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 1 Section G - Critical Angle and Total Internal Reflection (T.I.R.)
6 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 1 Section H - Prism
6 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 1 Section B, C, D, E - Mirror formula and Magnification, Velocity in Spherical Mirror, Cutting of Mirrors, Combination of Mirrors, Intensity of light
10 Videos
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-4 level-II
5 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - B Previous Years Problems
15 Videos
Similar Questions
Two parallel rays are travelling in a medium of refractive index μ1=43 . One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=32 The path difference between the two rays due to the glass slab will be
View SolutionA ray of light is incident at angle i on a rectangular slab of thickness t and refractive index μ. Show that the lateral displacement of the emergent ray is
x=tsini⎡⎢⎣1−cosi(μ2−sin2i)1/2⎤⎥⎦ Can x exceed t ?
View Solution
Knowledge Check
The time taken by a ray of light to travel through a glass slab of thickness 2 cm and refractive index 1.5 will be
A10^(-8) sB10−10sC2×10−8sD10−12sTwo parallel rays are travelling in a medium of refractive index μ1=4/3. One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=3/2. The path difference between the two rays due to the glass slab will be
A4t/3B3t/2Ct/8Dt/6The angle between the incident and the emergent ray from a glass slab is
A90∘B0∘Cless than 90∘Dmore than 90∘
A ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
View SolutionA ray of light enters a spherical drop of water of refractive index μ as shown in figure.
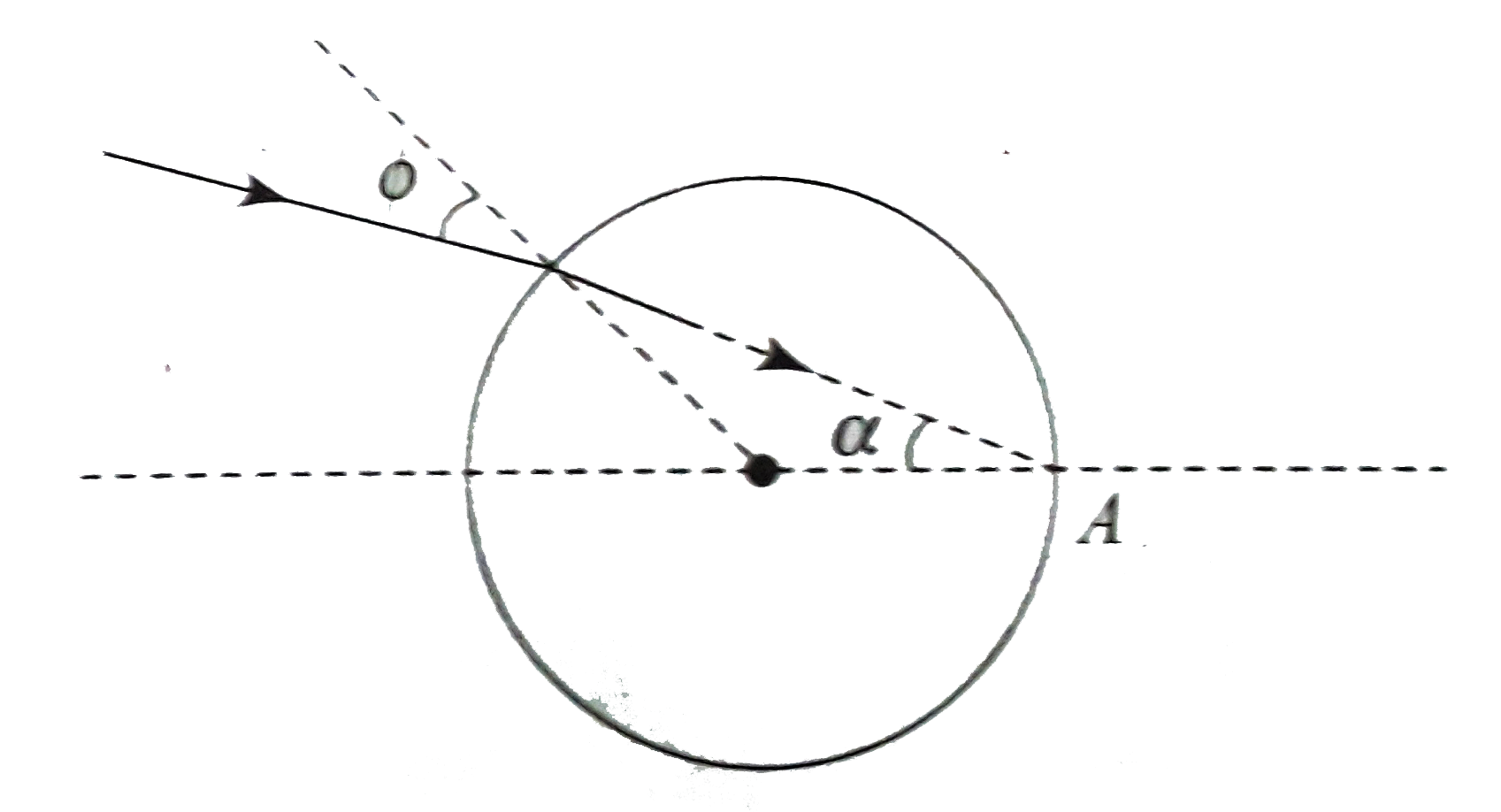
Q. An expression of the angle between incident ray and emergent ray (angle of deviation) as shown in figure.

View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA ray of lighyt is incident at an angle I on a glass slab of refractive index μ. The angle between reflected and refracted light is 90∘ Then the relationship between I and μ is
View SolutionA ray of light falls on a transparent glass slab of refractive index 1.62. What is the angle of incidence if the reflected ray and refracted ray are mutually perpendicular?
View Solution
