A small plane mirror is rotating at constant frequency of n rotations per second. With what linear velocity (in ms-1) will a light spot move along a spherical screen of radius of curvature of R metres if the mirror is at the centre of curvature of the screen?
The correct Answer is:4πnR
To solve the problem, we will follow these steps:
Step 1: Understand the rotation of the mirror
The mirror is rotating at a frequency of n rotations per second. This means that in one second, it completes n full rotations.
Hint: Remember that one full rotation corresponds to an angle of 2π radians.
Step 2: Calculate the angular velocity of the mirror
The angular velocity ω of the mirror can be calculated using the formula:
ω=2πn(in radians per second)
This is because for n rotations, the total angle covered is 2πn radians.
Hint: Angular velocity is the rate of change of angle with respect to time.
Step 3: Relate the angular velocity of the image to the mirror
When the mirror rotates by an angle ϕ, the light spot on the screen moves by an angle 2ϕ. Therefore, the angular velocity of the image ωimage is twice that of the mirror:
ωimage=2ω=2(2πn)=4πn
Hint: The relationship between the angles is crucial for finding the angular velocity of the image.
Step 4: Calculate the linear velocity of the light spot
The linear velocity v of the light spot on the spherical screen can be calculated using the formula:
v=r⋅ω
where r is the radius of curvature of the screen, which is given as R. Thus, substituting the angular velocity of the image:
v=R⋅(4πn)
Hint: Linear velocity is directly proportional to both the radius and the angular velocity.
Final Answer
The linear velocity of the light spot moving along the spherical screen is given by:
v=4πnR(in m/s)
The mirror is rotating at a frequency of n rotations per second. This means that in one second, it completes n full rotations.
The angular velocity ω of the mirror can be calculated using the formula:
ω=2πn(in radians per second)
This is because for n rotations, the total angle covered is 2πn radians.
When the mirror rotates by an angle ϕ, the light spot on the screen moves by an angle 2ϕ. Therefore, the angular velocity of the image ωimage is twice that of the mirror:
ωimage=2ω=2(2πn)=4πn
The linear velocity v of the light spot on the spherical screen can be calculated using the formula:
v=r⋅ω
where r is the radius of curvature of the screen, which is given as R. Thus, substituting the angular velocity of the image:
v=R⋅(4πn)
The linear velocity of the light spot moving along the spherical screen is given by:
v=4πnR(in m/s)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 3 | Level-I (Section B, C, D, E - Mirror formula and Magnification, Velocity in Spherical Mirror, Cutting of Mirrors, Combination of Mirrors, Intensity of light)7videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 3 | Level-I (Section F - Snells Law, Apparent depth and Normal shift, Refraction through a Glass slab, Lateral shift)4videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 2 (Level-II) Section M - Chromatic Aberration and Achromatism, Optical Instrument + Eye + Luminous Intensity2videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-4 level-II5videos
FLUID
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - B Previous Years Problems15videos
GRAVITATION
Similar Questions
Figure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is θ and the mirror is rotating clockwise with constant angular veloity ω. Find the speed of spot P at this instant.
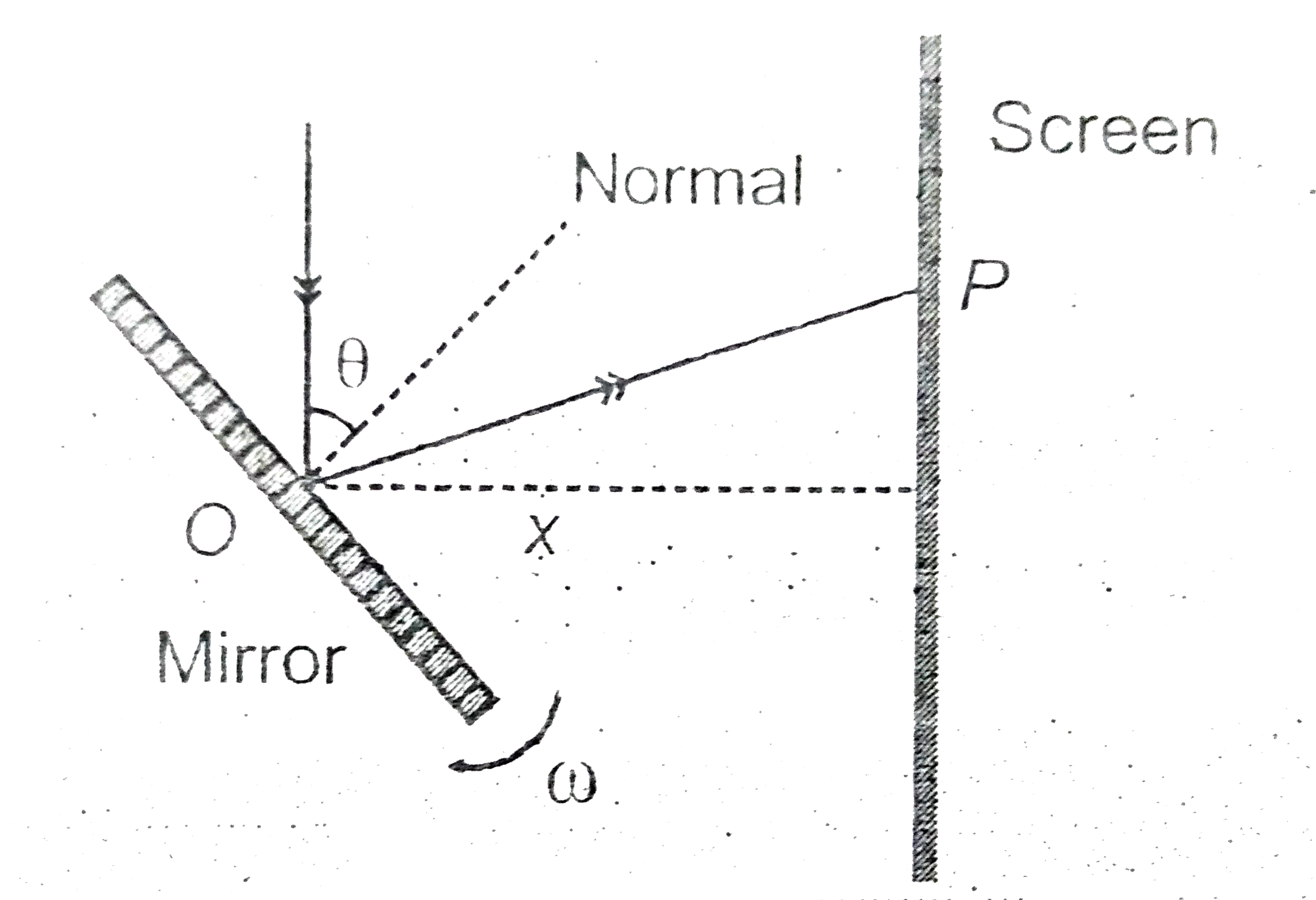 View Solution
View SolutionWhen an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that 1v+1u=1f, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio h'h is called linear magnification or lateral magnification and its value m is given as :
m=h'h=−vu
A small match box lies along the principal axis of a concave mirror and one end of match box is at centre of curvature of the mirror. Draw a ray diagram to show its image. Is its magnetification uniform?View Solution
Knowledge Check
- Question 1 - Select One
A flat mirror revolves at a constant angular velocity making n=0.4 revolutions per second. With what velocity (in m s−1) will a light spot move along a spherical screen with a radius of 15 m, if the mirror is at the centre of curvature of the screen ?
A37.7B60.3C68.7D75.4 - Question 2 - Select One
A charge q coulomb moves in a circle at n revolution per second and the radius of the circle is r metre. Then magnetic feild at the centre of the circle is
A2πqnr×10−7NA−1m−1B2πqr×10−7NA−1m−1C2πnqr×10−7NA−1m−1D2πqr×10−7NA−1m−1 - Question 3 - Select One
The separation between the screen and a concave mirror is 2 r . An isotropic point source of light is placed exactly midway between the mirror and the point source. Mirror has a radius of curvature r and reflects 100% of the incident light. Then the ratio of illuminances on the screen with and without the mirror is
A10:1B2:1C10:9D9:1
A small plane mirror kept at the centre of a sphere of diameter 3 m, makes 12 revolution per second. A thin light beam is made incident on the mirror. The linear speed of the light spot on the sphere, formed after reflection-from the mirror is:
View SolutionConsider a light source placed at a distance of 1.5 m along the aixs facing facing the convex side of a spherical mirror of radius of curvature 1m. The position (s), nature and magnification (m) of the image are
View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.

If fringe width is 0.1 mm then what is the wavelength of light used ?View SolutionA small plane mirror placed at the centre of a spherical screen of radius R. A beam of light is falling on the mirror, If the mirror makes n revolution per second, the speed of light on the screen after reflection from the mirror will be
View SolutionAssertion (A) : A ray of light passing through the centre of curvature of a spherical mirror retraces its path after reflection from the mirror.
Reason (R) : A ray of light passing through the centre of curvature of a spherical mirror is incident normally on the surface of the mirror.View Solution

