Consider a long infinite wire carrying a time varying current i=kt(k>0). A circular loop of radius a and resistance R is placed with its centre at a distance d from the wire (a<<d). Find out the induced current in the loop?
To find the induced current in a circular loop placed near a long infinite wire carrying a time-varying current, we can follow these steps:
Step 1: Identify the current in the wire
The current in the wire is given by the equation:
i(t)=kt
where k is a constant and t is time.
Step 2: Determine the magnetic field due to the wire
The magnetic field B at a distance d from a long straight wire carrying current I is given by:
B=μ0I2πd
Substituting I=kt into this formula, we have:
B=μ0(kt)2πd
Step 3: Calculate the magnetic flux through the loop
The magnetic flux Φ through the circular loop of radius a is given by:
Φ=B⋅A
where A is the area of the loop. The area A of the circular loop is:
A=πa2
Thus, substituting for B:
Φ=(μ0(kt)2πd)⋅(πa2)
This simplifies to:
Φ=μ0a2kt2d
Step 4: Find the induced emf
The induced electromotive force (emf) E in the loop can be found using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
Calculating the derivative:
E=−ddt(μ0a2kt2d)=−μ0a2k2d
Step 5: Calculate the induced current
Using Ohm's law, the induced current Iind in the loop is given by:
Iind=ER
Substituting the expression for E:
Iind=−μ0a2k2dR
Thus, the induced current is:
Iind=−μ0a2k2dR
Final Result
The induced current in the loop is:
Iind=−μ0a2k2dR
The current in the wire is given by the equation:
i(t)=kt
where k is a constant and t is time.
The magnetic field B at a distance d from a long straight wire carrying current I is given by:
B=μ0I2πd
Substituting I=kt into this formula, we have:
B=μ0(kt)2πd
The magnetic flux Φ through the circular loop of radius a is given by:
Φ=B⋅A
where A is the area of the loop. The area A of the circular loop is:
A=πa2
Thus, substituting for B:
Φ=(μ0(kt)2πd)⋅(πa2)
This simplifies to:
Φ=μ0a2kt2d
The induced electromotive force (emf) E in the loop can be found using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
Calculating the derivative:
E=−ddt(μ0a2kt2d)=−μ0a2k2d
Using Ohm's law, the induced current Iind in the loop is given by:
Iind=ER
Substituting the expression for E:
Iind=−μ0a2k2dR
Thus, the induced current is:
Iind=−μ0a2k2dR
The induced current in the loop is:
Iind=−μ0a2k2dR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-1
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (LEVEL-I)
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
- ELECTROMAGNETISMBOOK - MOTIONCHAPTER - ELECTROMAGNETISMEXERCISE - Exercise
136 Videos
Similar Questions
A circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
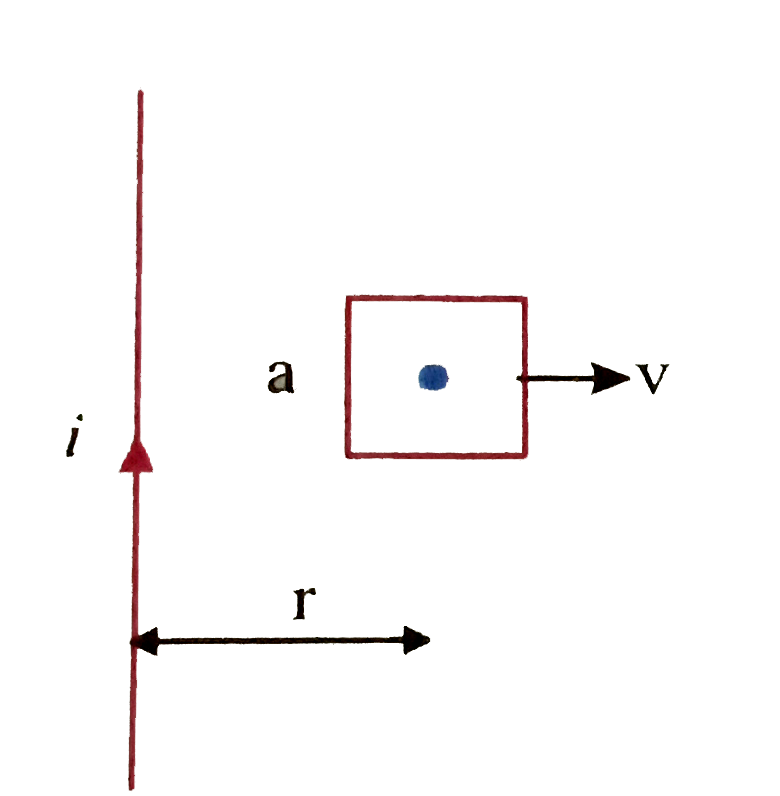
View Solution
Knowledge Check
What will be magnetic field at centre of current carrying circular loop of radius R?
Aμ0I4πRBμ0I2πRCμ0I2RDzeroA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
Amoved parallel to the wireBroatated about an axis perpendicular to the plane of the loop passing through the centre of the loopCrotated about an axis parallel to the wire passing through the centre of the loopDmoved away from the wireA loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
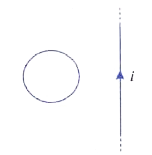 AclockwiseBanticlockwiseCzeroDcannot determine
AclockwiseBanticlockwiseCzeroDcannot determine
Two infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionA current i=αt , where t is time is flowing in a long wire. A smaller circular loop of radius a has its plane parallel to the wire and is placed at distance d from the wire. If resistance per unit length of loop is λ , find the magnitude and direction of the current in the loop.
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA straight wire carrying a current is turned into a circular loop if the magnitude of magnetic moment associated with it is M then the length of the wire will be
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop

View Solution
