Two parallel, long, straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angles so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. Now they start moving out with a constant velocity (v).
Will the current be time dependent?
To solve the problem step by step, we will analyze the situation involving the conductors, the magnetic field, and the induced electromotive force (emf) as well as the current flowing through the conductors.
Step 1: Understand the Configuration
We have two parallel long conductors lying on a smooth plane surface, and two other parallel conductors resting on them at right angles, forming a square of side length a. A uniform magnetic field B is present perpendicular to the plane of the conductors.
Hint: Visualize the arrangement of the conductors and the magnetic field to understand how they interact.
Step 2: Analyze the Motion of the Conductors
The conductors start moving outward with a constant velocity v. As they move, the area enclosed by the conductors changes over time.
Hint: Consider how the movement of the conductors affects the area of the square formed by them.
Step 3: Calculate the Area as a Function of Time
Initially, the area A of the square is a2. As the conductors move apart, the new side length of the square becomes a+2vt (since both sides are moving outwards). Therefore, the area as a function of time t is given by:
A(t)=(a+2vt)2
Hint: Remember that the area of a square is the square of its side length.
Step 4: Determine the Magnetic Flux
The magnetic flux Φ through the area is given by:
Φ=B⋅A(t)=B⋅(a+2vt)2
Hint: Magnetic flux depends on both the magnetic field strength and the area it penetrates.
Step 5: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced emf E is given by:
E=−dΦdt
Calculating the derivative, we get:
E=−ddt(B(a+2vt)2)
Using the chain rule, we find:
E=−B⋅2(a+2vt)⋅(2v)=−4Bv(a+2vt)
Hint: The negative sign indicates the direction of the induced emf according to Lenz's law.
Step 6: Determine if the Induced EMF is Time-Dependent
Since the expression for induced emf E=−4Bv(a+2vt) contains t, it is clear that the induced emf is time-dependent.
Hint: Check if the expression for emf includes any variable that changes with time.
Step 7: Analyze the Current
Now, we need to determine if the current I is time-dependent. The resistance R of the circuit can be expressed as:
R=λ⋅L
where L is the length of the conductors, which increases as a+2vt. Thus,
R=λ⋅(4(a+2vt))
Using Ohm's law, the current I can be calculated as:
I=ER=−4Bv(a+2vt)λ⋅(4(a+2vt))
This simplifies to:
I=−Bvλ
Hint: Check if the current expression depends on time or remains constant.
Conclusion
The induced emf is time-dependent, while the current I is not time-dependent. Therefore, the answer to the question is:
Induced EMF: Yes, it is time-dependent.
Current: No, it is not time-dependent.
We have two parallel long conductors lying on a smooth plane surface, and two other parallel conductors resting on them at right angles, forming a square of side length a. A uniform magnetic field B is present perpendicular to the plane of the conductors.
The conductors start moving outward with a constant velocity v. As they move, the area enclosed by the conductors changes over time.
Initially, the area A of the square is a2. As the conductors move apart, the new side length of the square becomes a+2vt (since both sides are moving outwards). Therefore, the area as a function of time t is given by:
A(t)=(a+2vt)2
The magnetic flux Φ through the area is given by:
Φ=B⋅A(t)=B⋅(a+2vt)2
According to Faraday's law of electromagnetic induction, the induced emf E is given by:
E=−dΦdt
Calculating the derivative, we get:
E=−ddt(B(a+2vt)2)
Using the chain rule, we find:
E=−B⋅2(a+2vt)⋅(2v)=−4Bv(a+2vt)
Since the expression for induced emf E=−4Bv(a+2vt) contains t, it is clear that the induced emf is time-dependent.
Now, we need to determine if the current I is time-dependent. The resistance R of the circuit can be expressed as:
R=λ⋅L
where L is the length of the conductors, which increases as a+2vt. Thus,
R=λ⋅(4(a+2vt))
I=ER=−4Bv(a+2vt)λ⋅(4(a+2vt))
This simplifies to:
I=−Bvλ
The induced emf is time-dependent, while the current I is not time-dependent. Therefore, the answer to the question is:
Current: No, it is not time-dependent.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-125videos
ELECTROMAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (LEVEL-I)16videos
ELECTROMAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)8videos
ELECTRO MAGNETIC WAVES
- BOOK - MOTIONCHAPTER - ELECTROMAGNETISMEXERCISE - Exercise136videos
ELECTROMAGNETISM
Similar Questions
Two parallel, long, straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angles so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. Now they start moving out with a constant velocity (v).
Will the induced emf be time dependent?View SolutionTwo parallel, long, straight conductor lie on a smooth plane surface. Two other parallel so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the cinductors. Now they start moving out with a constant velocity v.
(A) Will the induced emf be time dependent?
(b) Will the current be time dependent ?View Solution
Knowledge Check
- Question 1 - Select One
Two parallel long straight conductors lie on a smooth surface. Two other parallel conductors rest on them at right angless so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. They all start moving out with a constant velocity v. If r is the resistance per unit length of the wire the current in the circuit will be
ABvrBBrvCBvrDBv - Question 2 - Select One
Two parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward with a constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
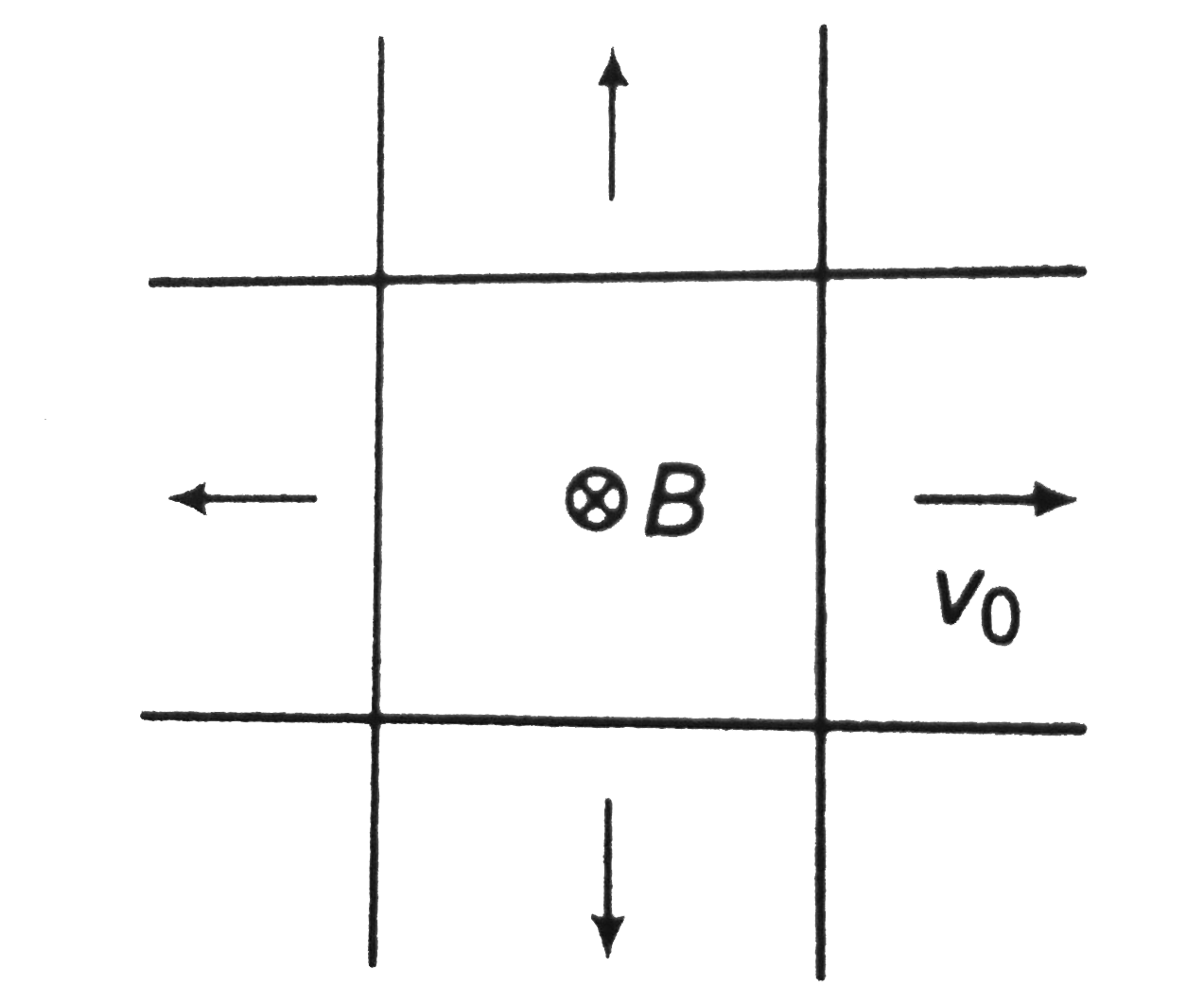 AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ
AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ - Question 3 - Select One or More
Two parallel long straight conductors lie on a smooth horizontal surface. Two other parallel conductor rest on them at right angles so as from B exits vertical. A uniform magnetic field B exists a vertical direction. Now all the four conductors stock moving outwards with a constant velocity v. The induced emf e and induced current i will vary wide time t as
A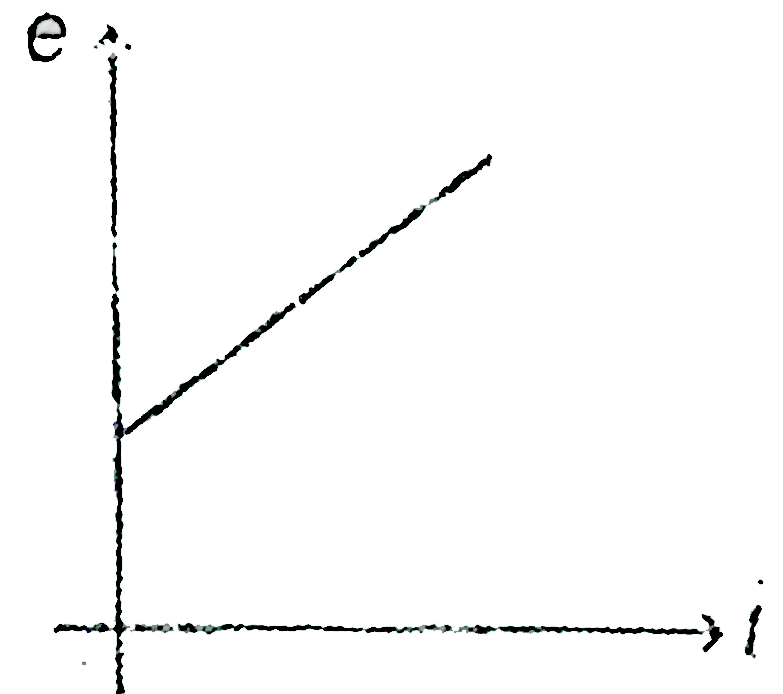 B
B C
C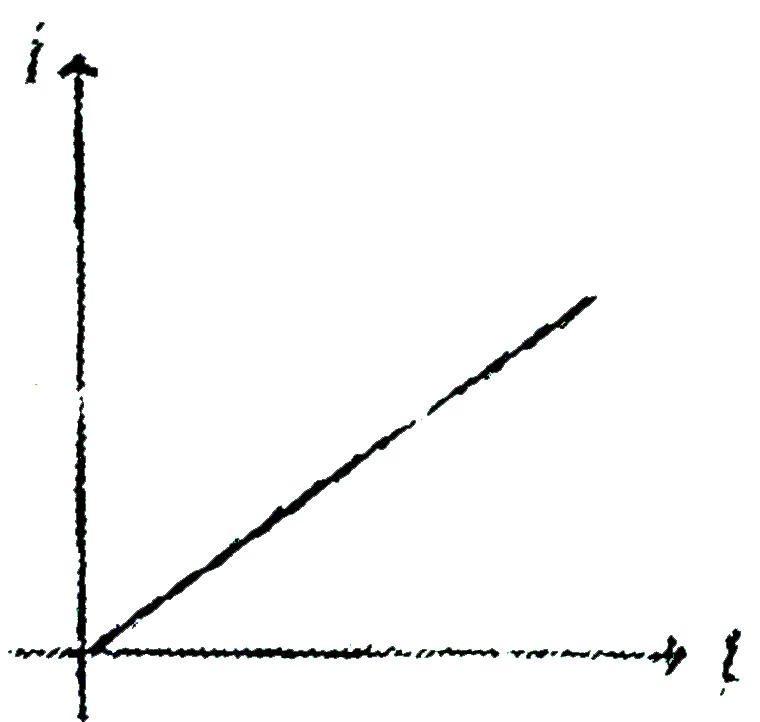 D
D
An electron and a proton moving parallel to each other in the same direction with equal momentra, enter into a uniform magnetic field which is at right angles to their velocities. Trace their trajectories in the magnetic field.
View SolutionA conductor in the form of a right angle ABC with AB=3cm and BC=4cm carries a current of 10A.There is a uniform magnetic field of 5T perpendicular to the palne of the conductor. The force on the conductor will be
View SolutionA square conducting loop of side L and resistance R is moving with a uniform velocity at right angles to one of the side in its own plane . On applying a uniform magnetic field at right angles to its plane as show in the figure the induced current in the loop will be __
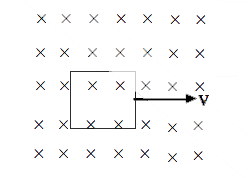 View Solution
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
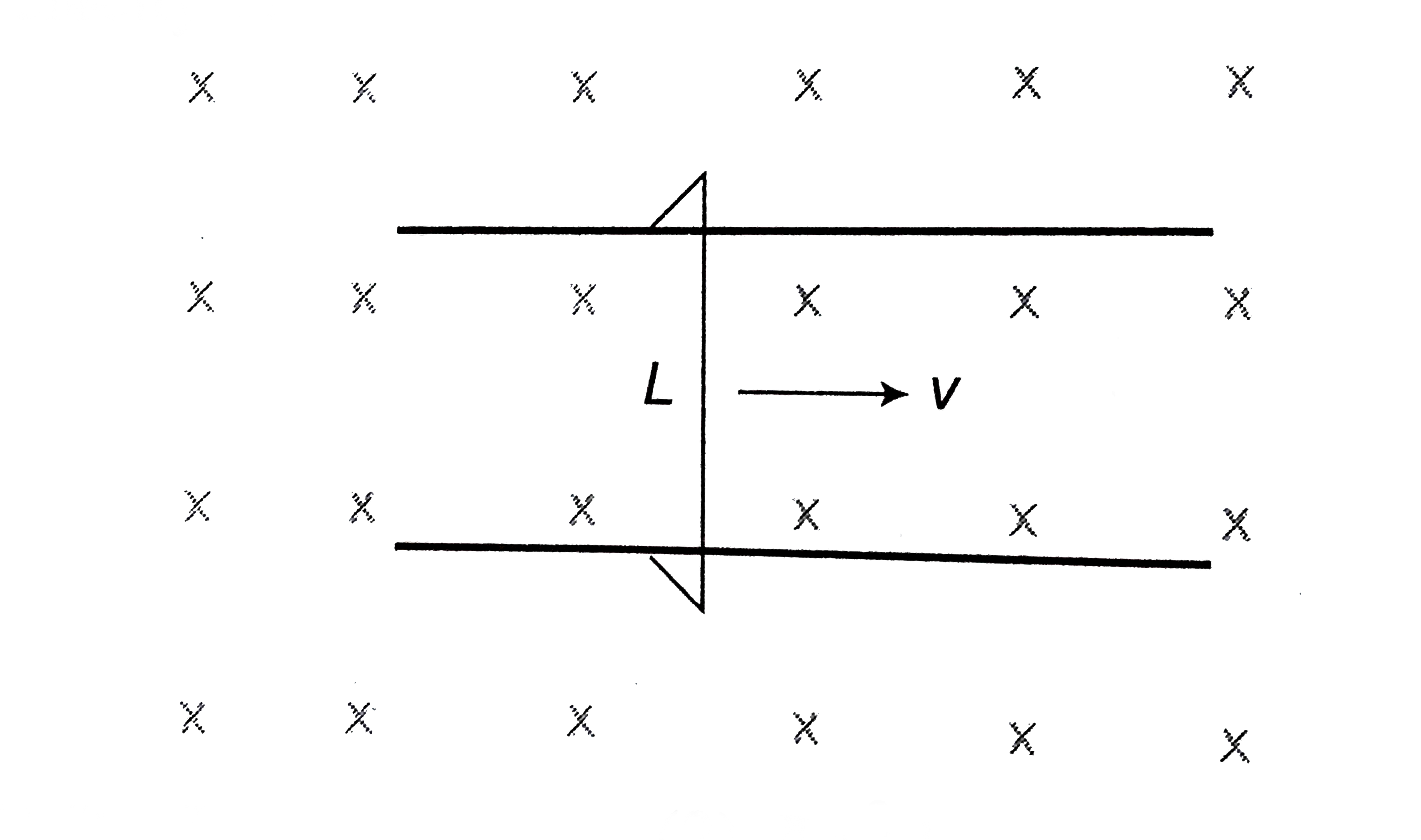 View Solution
View SolutionTwo idential conductors P and Q are placed on two frictionless rails R and S in a uniform magnetic field directed into the plane. If P is moved in the direction shown in figure with a constant speed, then rod Q
 View Solution
View Solution

