A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
To solve the problem of finding the induced emf in a rod of length l that is moved parallel to a long wire carrying current i, we can follow these steps:
Step 1: Understand the Setup
We have a long straight wire carrying a current i. A rod of length l is placed perpendicular to this wire, and its nearest end is at a distance a from the wire. The rod is moving parallel to the wire with a velocity v.
Step 2: Magnetic Field Due to the Wire
The magnetic field B at a distance x from a long straight wire carrying current i is given by the formula:
B=μ0I2πx
where μ0 is the permeability of free space.
Step 3: Consider a Differential Element of the Rod
Let's consider a small element of the rod of length dx at a distance x from the wire. The magnetic field at this distance is:
B(x)=μ0I2πx
Step 4: Calculate the Induced EMF in the Differential Element
The induced emf dE in the small element dx of the rod moving with velocity v can be calculated using the formula:
dE=B⋅L⋅v
Substituting for B and L=dx:
dE=(μ0I2πx)⋅dx⋅v
Step 5: Integrate to Find Total Induced EMF
To find the total induced emf E in the entire rod, we need to integrate dE from x=a to x=a+l:
E=∫a+laμ0Iv2πxdx
Step 6: Perform the Integration
The integral of 1x is lnx:
E=μ0Iv2π(lnx)a+la
This evaluates to:
E=μ0Iv2π(ln(a+l)−ln(a))
Using the property of logarithms:
ln(a+l)−ln(a)=ln(a+la)
Thus, we have:
E=μ0Iv2πln(a+la)
Final Answer
The induced emf in the rod is:
E=μ0Iv2πln(a+la)
We have a long straight wire carrying a current i. A rod of length l is placed perpendicular to this wire, and its nearest end is at a distance a from the wire. The rod is moving parallel to the wire with a velocity v.
The magnetic field B at a distance x from a long straight wire carrying current i is given by the formula:
B=μ0I2πx
where μ0 is the permeability of free space.
Let's consider a small element of the rod of length dx at a distance x from the wire. The magnetic field at this distance is:
B(x)=μ0I2πx
The induced emf dE in the small element dx of the rod moving with velocity v can be calculated using the formula:
dE=B⋅L⋅v
Substituting for B and L=dx:
dE=(μ0I2πx)⋅dx⋅v
To find the total induced emf E in the entire rod, we need to integrate dE from x=a to x=a+l:
E=∫a+laμ0Iv2πxdx
The integral of 1x is lnx:
E=μ0Iv2π(lnx)a+la
This evaluates to:
E=μ0Iv2π(ln(a+l)−ln(a))
Using the property of logarithms:
ln(a+l)−ln(a)=ln(a+la)
Thus, we have:
E=μ0Iv2πln(a+la)
The induced emf in the rod is:
E=μ0Iv2πln(a+la)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-1
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (LEVEL-I)
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
- ELECTROMAGNETISMBOOK - MOTIONCHAPTER - ELECTROMAGNETISMEXERCISE - Exercise
136 Videos
Similar Questions
A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View Solution
Knowledge Check
Figure shows an irregular shapped wire AB moving with velocity v. Find the emf induced in the wire :-
AVBlsinθBV2BlsinθCVBlcosθDVBlElectric charge q is distributed uniformly over a rod of length l. The rod is placed parallel to a ling wire carrying a current i. The separation between the rod and the wire is . The force needed to move the rod along its length with a uniform velocity v is
Aμ0iqv2πaBμ0iqv4πaCμ0iqvl2πaDμ0iqvl4πaThe current carrying wire and the rod AB are in the same plane. The rod moves parallel to the wire with a velocity v . Which one of the following statements is true about induced emf in the rod
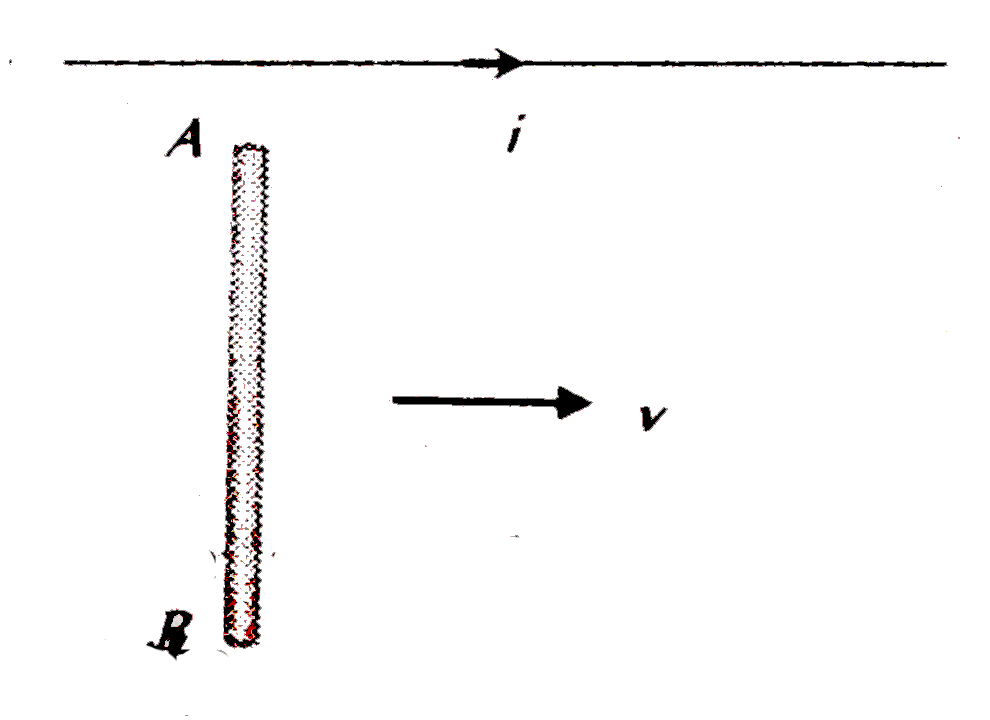 AEnd A will be at lower potential with respect to BBA and B will be at the same potentialCThere will be no induced e.m.f. in the rodDPotential at A will be higher than that at B
AEnd A will be at lower potential with respect to BBA and B will be at the same potentialCThere will be no induced e.m.f. in the rodDPotential at A will be higher than that at B
Shows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.

View SolutionElectric charge q is uniformly distributed over a rod of length / The rod is placed parallel to a long wire carrying a current I The separation between the rod and the wire is a find the force needed to move the rod along its length with a uniform velocity v
View SolutionWire carrying a study current and rod AB are in the same plane the rod move parallel to wire with velocity v then which end of the rod is at higher potential.
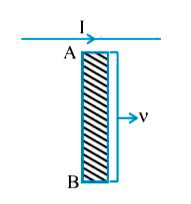
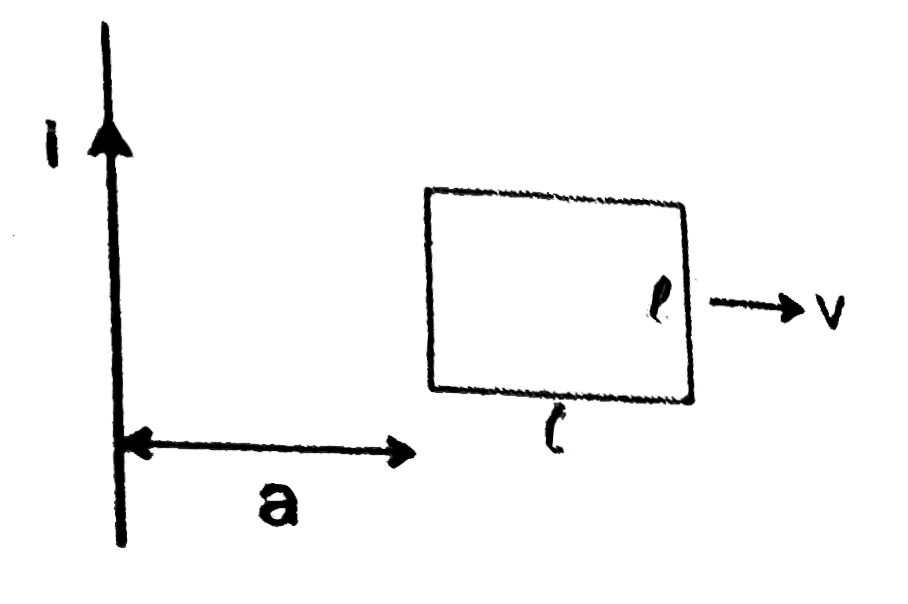
View SolutionA square meallic loop of side l is placed near a fixed long wire carrying a current i (figure). The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop. The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ. Find out value of x .
View SolutionA conducting rod length 1m moves with a speed of 2m/s parallel to a straight long wire carrying 4A current. Axis of rod is kept perpendicular to the wire with its near end at a distance of 1m from the wire. Magnitude of induced emf in rod is N×10−7log16volt. Find the value of N.
View Solution
