A point positive charge of Q' units is moved round another point positive charge of Q units in circular path. If the radius of the circle r is the work done on the charge Q' in making one complete revolution i-
Q4π∈0r
QQ'4π∈0r
Q'4π∈0r
0
The correct Answer is:D
To find the work done on a point positive charge Q′ when it is moved around another point positive charge Q in a circular path of radius r, we can follow these steps:
Step 1: Understand the Forces Involved
When a positive charge Q′ is placed near another positive charge Q, they repel each other due to the electrostatic force. The force F between the two charges can be calculated using Coulomb's law:
F=kQ⋅Q′r2
where k is Coulomb's constant.
Step 2: Analyze the Motion
As Q′ moves in a circular path around Q, the direction of the force F is always directed radially outward from Q to Q′. The motion of Q′ is tangential to the circular path.
Step 3: Determine the Work Done
The work done dW on the charge Q′ when it moves a small distance ds in the direction of the force F is given by:
dW=F⋅ds
However, since the force F is always directed outward and the displacement ds is tangential to the circular path, the angle θ between the force and displacement is 90∘.
Step 4: Calculate the Work Done
Since the angle θ is 90∘, we have:
cos(90∘)=0
Thus, the work done for a small displacement becomes:
dW=F⋅ds⋅cos(90∘)=0
This means that the work done in moving Q′ through any small segment of the circular path is zero.
Step 5: Total Work Done for One Complete Revolution
Since the work done for each infinitesimal segment of the path is zero, the total work done W in making one complete revolution around the charge Q is:
W=∫dW=0
Conclusion
The work done on the charge Q′ in making one complete revolution around the charge Q is zero.
When a positive charge Q′ is placed near another positive charge Q, they repel each other due to the electrostatic force. The force F between the two charges can be calculated using Coulomb's law:
F=kQ⋅Q′r2
where k is Coulomb's constant.
As Q′ moves in a circular path around Q, the direction of the force F is always directed radially outward from Q to Q′. The motion of Q′ is tangential to the circular path.
The work done dW on the charge Q′ when it moves a small distance ds in the direction of the force F is given by:
dW=F⋅ds
However, since the force F is always directed outward and the displacement ds is tangential to the circular path, the angle θ between the force and displacement is 90∘.
Since the angle θ is 90∘, we have:
cos(90∘)=0
Thus, the work done for a small displacement becomes:
dW=F⋅ds⋅cos(90∘)=0
This means that the work done in moving Q′ through any small segment of the circular path is zero.
Since the work done for each infinitesimal segment of the path is zero, the total work done W in making one complete revolution around the charge Q is:
W=∫dW=0
The work done on the charge Q′ in making one complete revolution around the charge Q is zero.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)
64 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)
41 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
A charged particle is moving in a circular path under the action of the Lorentz force. How much work is done by the force in one revolution?
View SolutionWhat is the amount of work done in moving a point charge around a circular arc of radius r at the centre of which another point charge is located?
View Solution
Knowledge Check
A point charge Q is moved along a ciruclar path around another fixed point charge. The work done is zero
Aonly if Q returns to its starting pointBonly if the twoi charges have the same magnitudeConly if the two charges have the same magnitude and opposite signsDin all caseIn the firgure the charge Q is at the centre of the circle. Work done is maximum when another charge is taken from point P to
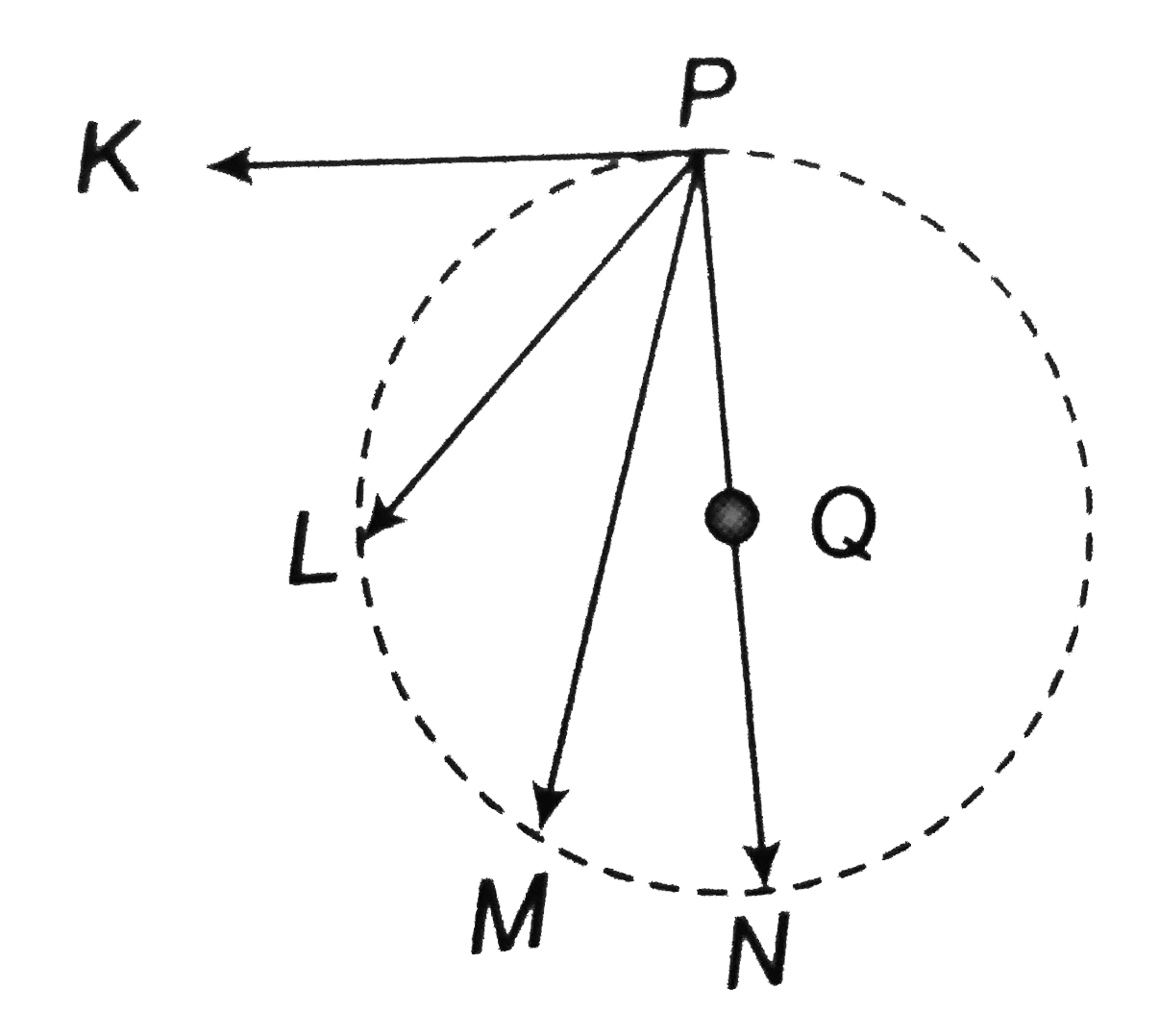 AKBLCMDN
AKBLCMDNThere is 10 units of charge at the centre of a circle of radius 10m. The work done in moving 1 unit of charge around the circle once is
AzeroB10 unitsC100 unitsD1 unit
What is the amount of work done in moving a point charge q0 around a circular arc of radius 'r' at the centre of which another point charge q is located ?
View SolutionA particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View SolutionA unit positive charge is moved along the circumfer-ence of a circle of radius, r with a −5μC charge at the centre at the centre of the circle. Then, the work done in the process is ______.
View SolutionA point charge -q is moving around another charge Q under the electrostatic attraction. If the path followed is elliptical, then
View SolutionAn agent is moving a positively charged body towards another fixed positive charge. The work done by the agent is
View Solution
