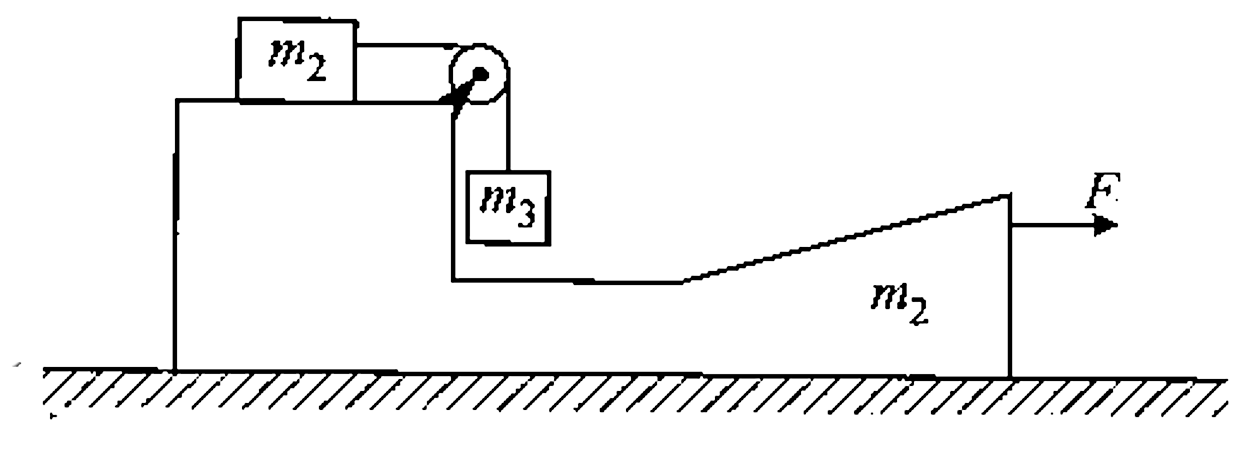
All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–

(m1+m2+m3)m2gm1
(m1+m2)m2gm1
(m2+m3)m1gm2
(m1+m3)m1gm2
The correct Answer is:A
Step by step video, text & image solution for All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m_(1) and m_(2) do not move relative to m_(3) is :– by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-C :- Pseudo force, Weighing Machine
Explore 2 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-D :- Spring force and spring cutting problems
Explore 1 Video
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems
Explore 23 Videos
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-4 ( LEVEL- II)
Explore 39 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-4 ( LEVEL-II)
Explore 15 Videos
Similar Questions
Knowledge Check
A large cubical shaped block of mass M rests on a fixed horizontal surface. Two blocks of mass m1 and m2 are connected by a light inextensible string passing over a light pulley as shown. Neglect friction everywhere. Then the constant horizontal force of magnitude F that should be applied to M so that m1 and m2 do not mov relative toM is:
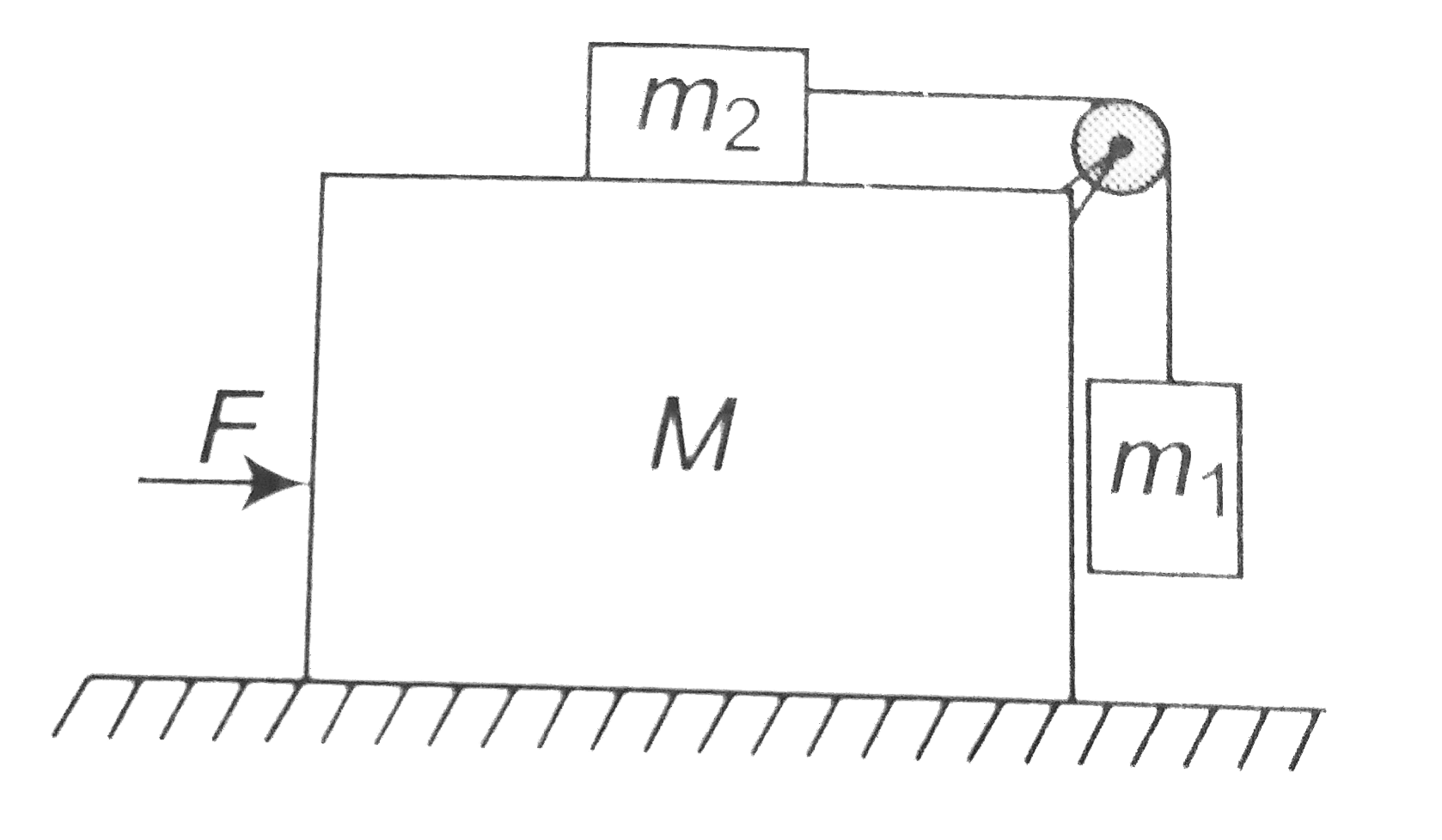 AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)g
AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)gTwo blocks of mass m1=6kg and m2=3kg are as shown in the diagram. Coefficient of friction between m1 and m2 and between m1 and m2 and between m1 and the surface is 0.5 and 0.4 , respectively . The maximum horizontal force that can be applied to the mass m1 so that they move without separation is
 A41NB61NC81ND101N
A41NB61NC81ND101NFor the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

Let F1 and F2 are applied in such a way that m1andm2 do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m1>m2.A(m1+m2)gM+m1+m2B(m1−m2)gMC(m1−m2)gM+m1+m2DF1−F2M
Column 1 gives four different situations involving two blocks of mass m1andm2 placed in different ways on smooth horizontal surface as shown. In each of the situations, horizontal forces F1andF2 are applied on blocks of mass m1andm2, respectively and also m2F1<m1F2. Match the statements in column I with the corresponding results in column II.

View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View SolutionA block of mass 100 kg is set into motion on a frictionless horizontal surface with the help of a frictionless pulley and rope system shown in What horizontal force should be applied on the rope to produce an acceleration of 0.1m/s2
 .
.
View SolutionIn the adjoining figure all surface are frictionless . What force F must by applied to M1 to keep M3 free from rising or falling?

View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is μ=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

View Solution