A coil of N turns having cross sectional area A, and resistance 'R' placed in transverse uniform magnetic fiel B . If it is rotates about its one of the diameter through an angle 'θ' in time interval 't'
Find following induced parameters in coil :-
To solve the problem, we will find the induced EMF, induced current, and induced charge in a coil that is rotating in a magnetic field.
1. Understanding the Initial Magnetic Flux:
The initial magnetic flux (Φi) associated with the coil is given by:
Φi=B⋅A⋅cos(0∘)=B⋅A
where B is the magnetic field strength, and A is the cross-sectional area of the coil.
Hint: Remember that the cosine of 0 degrees is 1, which simplifies the initial flux calculation.
2. Calculating the Final Magnetic Flux:
After rotating the coil through an angle θ, the final magnetic flux (Φf) is:
Φf=B⋅A⋅cos(θ)
Hint: The angle θ is the angle between the magnetic field and the area vector after rotation.
3. Finding the Change in Magnetic Flux:
The change in magnetic flux (ΔΦ) is:
ΔΦ=Φf−Φi=B⋅A⋅cos(θ)−B⋅A=B⋅A⋅(cos(θ)−1)
Hint: This step involves subtracting the initial flux from the final flux.
4. Calculating the Induced EMF:
According to Faraday's law of electromagnetic induction, the average induced EMF (E) is given by:
E=−nΔΦΔt=−nB⋅A⋅(cos(θ)−1)t
Simplifying this, we get:
E=−n⋅B⋅At(1−cos(θ))
Hint: The negative sign indicates the direction of the induced EMF according to Lenz's law.
5. Finding the Induced Current:
The induced current (I) in the coil can be calculated using Ohm's law:
I=ER=−n⋅B⋅At(1−cos(θ))R
Thus, the induced current is:
I=−n⋅B⋅AR⋅t(1−cos(θ))
Hint: Make sure to use the resistance R of the coil in this calculation.
6. Calculating the Induced Charge:
The total induced charge (Q) can be calculated using the relationship between current and charge:
Q=I⋅t=(−n⋅B⋅AR⋅t(1−cos(θ)))⋅t
Simplifying gives:
Q=−n⋅B⋅AR(1−cos(θ))
Hint: The total charge is the product of current and time, so the time t cancels out in the expression.
Summary of Induced Parameters:
- Induced EMF:
E=−n⋅B⋅At(1−cos(θ))
- Induced Current:
I=−n⋅B⋅AR⋅t(1−cos(θ))
- Induced Charge:
Q=−n⋅B⋅AR(1−cos(θ))
The initial magnetic flux (Φi) associated with the coil is given by:
Φi=B⋅A⋅cos(0∘)=B⋅A
where B is the magnetic field strength, and A is the cross-sectional area of the coil.
After rotating the coil through an angle θ, the final magnetic flux (Φf) is:
Φf=B⋅A⋅cos(θ)
The change in magnetic flux (ΔΦ) is:
ΔΦ=Φf−Φi=B⋅A⋅cos(θ)−B⋅A=B⋅A⋅(cos(θ)−1)
According to Faraday's law of electromagnetic induction, the average induced EMF (E) is given by:
E=−nΔΦΔt=−nB⋅A⋅(cos(θ)−1)t
Simplifying this, we get:
E=−n⋅B⋅At(1−cos(θ))
The induced current (I) in the coil can be calculated using Ohm's law:
I=ER=−n⋅B⋅At(1−cos(θ))R
Thus, the induced current is:
I=−n⋅B⋅AR⋅t(1−cos(θ))
The total induced charge (Q) can be calculated using the relationship between current and charge:
Q=I⋅t=(−n⋅B⋅AR⋅t(1−cos(θ)))⋅t
Simplifying gives:
Q=−n⋅B⋅AR(1−cos(θ))
- Induced EMF:
E=−n⋅B⋅At(1−cos(θ))
- Induced Current:
I=−n⋅B⋅AR⋅t(1−cos(θ))
- Induced Charge:
Q=−n⋅B⋅AR(1−cos(θ))
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - QUESTION FOR PRACTICE
41 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-1
72 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - QUESTIONS FOR PRACTICE (Type-III: Special Question :-)
2 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
Similar Questions
A circular coil of radius 2cm and 200 numbers of turns is placed perpendicular to uniform magnetic field of 2 T. The coil is turned through angle 180∘ in time interval of 0.5 s. What will be the average emf induced in the coil ?
View SolutionA coil of N turns and area A is placed in a uniform transverse magnetic field B in such a way that →Aand→B are parallel. If the plate in turned through 180∘ about its one of the diameter in 2 seconds then the (i) change of magnetic flux through the coil is ? (ii) rate of change of flux is the coil is ?
View Solution
Knowledge Check
A coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
A12 nBAωB32 nBAωC3 nBAωDnBAωA flat circular coil of n turns, area A and resitance R is placed in a uniform magnetic field B. The pane of coil is initially perpedicular of B. when the coil is rotated through an angle of 180∘ about one of its diameter, a charge Q1 flows through the coil When the same coil after charge Q2 flows through it. then Q2/Q1 is
A1B2C1/2D0A flat coil of n turns, area A and carrying a current I is placed in a uniform magnetic field of magnitude B. The plane of the coil makes an angle θ with the direction of the field. The torque acting on the coil is
ABInAsinθBnAIBsinθCBInAcosθDBIn2Acosθ
A rectangular coil ABCD is rotated in uniform magnetic field with constant angular velocity about its one of the diameter as shown in figure. The induced emf will be maximum, when the plane of the coil is :-
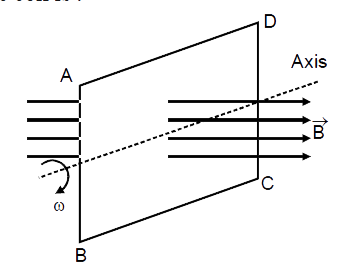
View SolutionA coil having n turns and area A is initially placed with its plane normal to the magnetic field B. It is then rotated through 180∘ in 0.2 sec. The emf induced at the ends of the coils is ___
View SolutionA coil of N turns and mean cross-sectional area A is rotating with uniform angular velocity ω about an axis at right angle to uniform magnetic field B. The induced emf E in the coil will be
View SolutionA flat coil, C, of n turns, area A and resistance R, is placed in a uniform magnetic field of magnitude B. The plane of the coil is initially perpendicular to B. The coil,is rotated by an angle θ about a diameter and charge of amount Q flows through it. Choose the correct alternatives.
View SolutionA circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of ω, about its own axis , then the induced emf in the coil is __
View Solution
