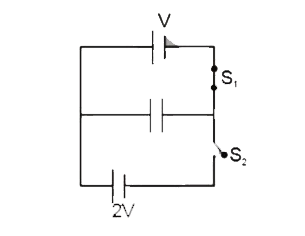
At any time S1 switch is opened and S2 is closed then find out heat generated in circuit.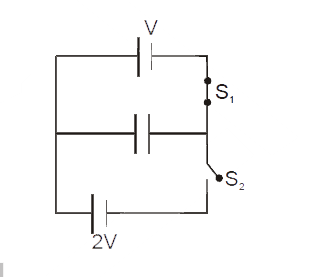 
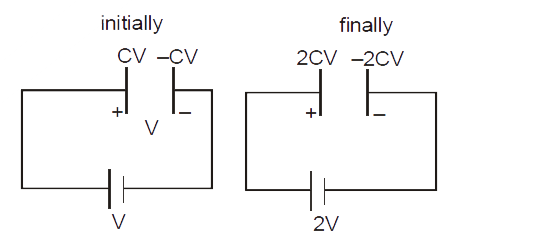
Charge flow through battery =Qf−Qi
=2CV-CV=CV
H=(CV×2V)−{12C(2V)2−12CV2}
=2CV2−{2CV2−12CV2}
H=12CV2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor.Then
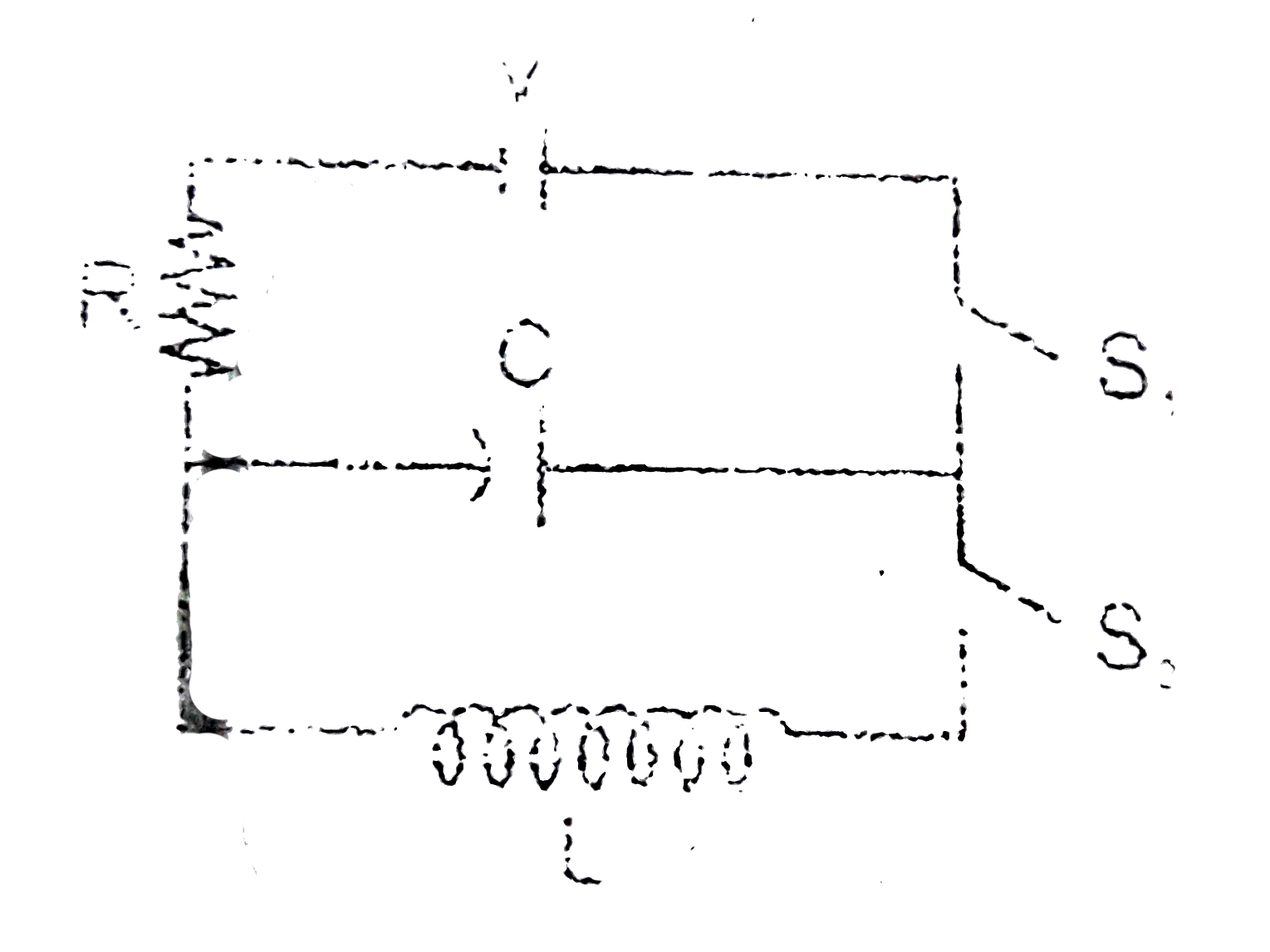Aat t=0,energy stored in the circuit is purely in the form of magnetic energyBat any time t>0,current in the circuit is in the same directionCat t>0,there is no exchange of energy between the inductor and capacitorDat any time t>0 instanteous curren in the circuit will have maximum vlaue V√CL ,where C is the capacitance and L is the inductance.In the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is
A10−6AB7.2μAC720μAD360μA
In given circuit initially switch Sw1 is closed and Sw2 is open, Now Sw1 is opened and Sw2 is closed, what is the heat liberated in resistance R?
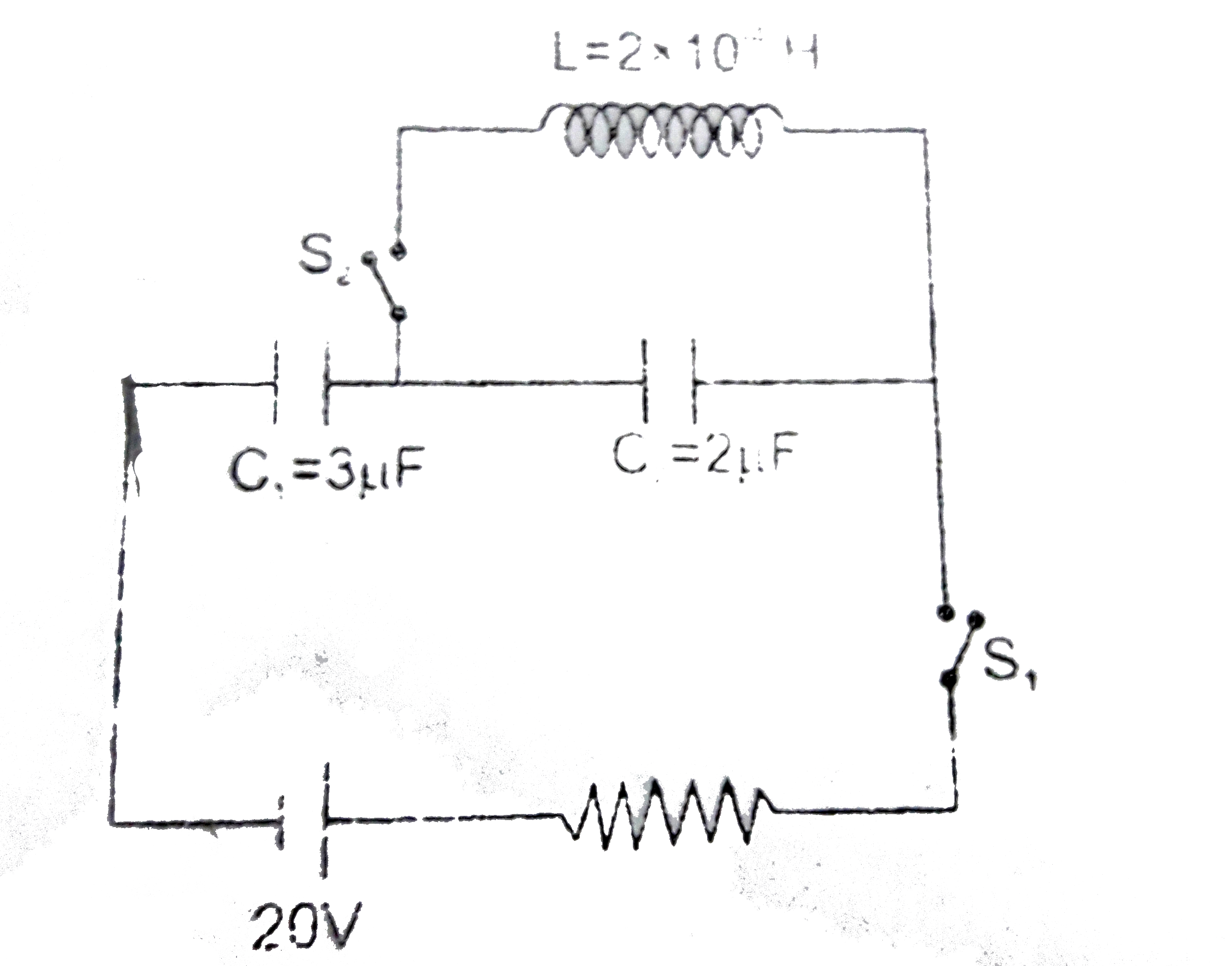
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.
Find the first instant t, when energy in inductor becomes one third of that in capacitor
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
View SolutionIn the circult shown
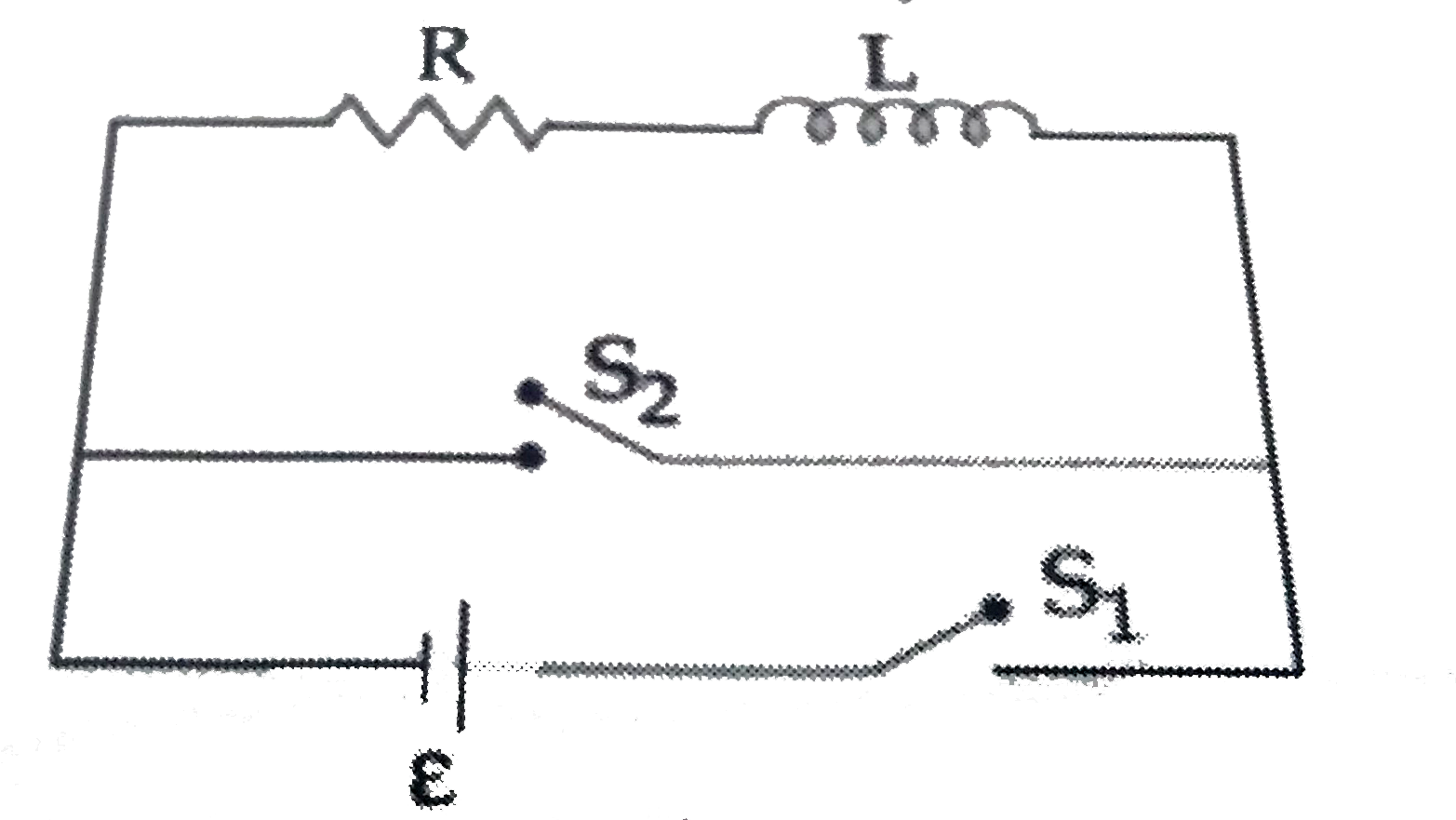the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
View SolutionAt t=0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
(i) The current through the capacitor immediately after that moment
(ii) Charge on the capacitor long after that moment.
(iii) Total charge flown through the cell of emf 2ε after S2 is closed.
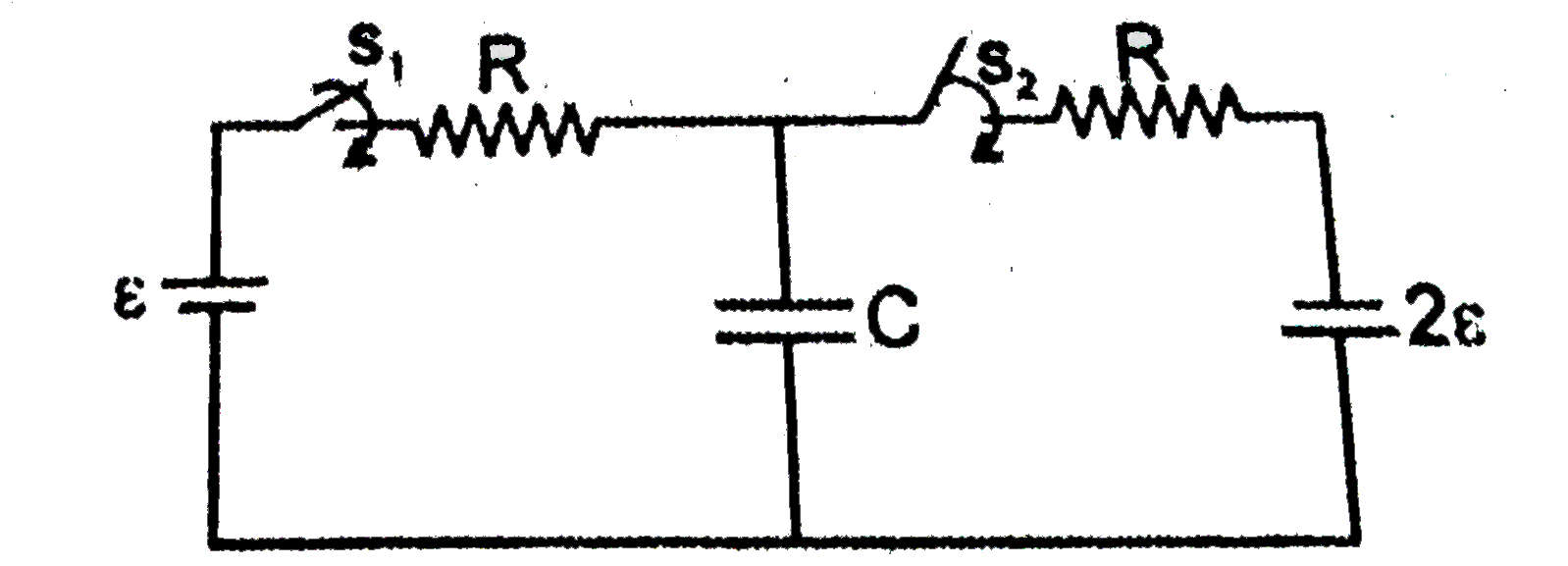
View SolutionAt t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
Charge on the capacitor long after that moment.
View Solution